定义和含义

分数，如果从乘法和除法的角度来定义分数，我们说 [math]\displaystyle{ \frac{1}{5} }[/math] 是那个乘以5以后得到1的数， [math]\displaystyle{ \frac{1}{5} }[/math] 也是那个1除以5以后得到的数。这时候，我们把除号称作"分数线"，也就是中间那条横线。有了分数线，我们把分数线上面的被除数称作"分子"，分数线下面的除数称作"分母"。

从而更进一步，我们用代数的思想来提炼一下，类似地，对于任何一个整数n，我们都可以通过除法和乘法计算来得到 [math]\displaystyle{ \frac{1}{n} }[/math] 。 [math]\displaystyle{ \frac{1}{n} }[/math] 是那个乘以n以后得到1的数，[math]\displaystyle{ \frac{1}{n} }[/math]也是那个1除以n以后得到的数^[1]。更更近一步，类似地，任何一个分数[math]\displaystyle{ \frac{m}{n} }[/math]都是[math]\displaystyle{ \frac{1}{n} }[/math]乘以m以后得到的数^[1]，也就是:

有了代数的基础后，从倍数的角度来说，指的是，也就是问某个东西的数量a是另一个东西的数量b的多少倍，然后我们可以用分数的形式把这个关系纪录下来，记作 [math]\displaystyle{ \frac{a}{b} }[/math] 。

如果从整体和部分的角度来看，分数，指的是，分子占分母的多少，也就是把分母看作一个整体，看作一个单位，蕴含着单位一的思想。这部分其实在倍数的知识中也有提及，复习一下看看吧。

层次标注

在这里，它属于第二层知识，即学科概念。

辅助理解的解释

为了避免你还没有学会代数，我们来举一个例子：

例如2个苹果是4个苹果的多少倍，我们按照倍数的含义，2是被除数，4是除数，于是我们记作： [math]\displaystyle{ 2 \div 4 \, }[/math] (倍)，然后我们可以用分数的形式把这个关系纪录下来，记作 [math]\displaystyle{ \frac{2}{4} }[/math] ，其中，我们把中间那条横线叫作分数线，分数线上面的2叫作分子，分数线下面的4叫作分母。

从倍数的知识出发，我们发现计算一个东西的数量a是另一个东西的数量b的多少倍时，我们是把a当作被除数，把b当作除数，于是我们可以写成 [math]\displaystyle{ a \div b \quad }[/math] (倍)。对比起分数 [math]\displaystyle{ \frac{a}{b} }[/math] 的形式，你有没有发现什么奥秘？

分数，不过就是，把除法换了一个形式，分数线就相当于除号，分子就是被除数，分母就是除数，仅此而已。

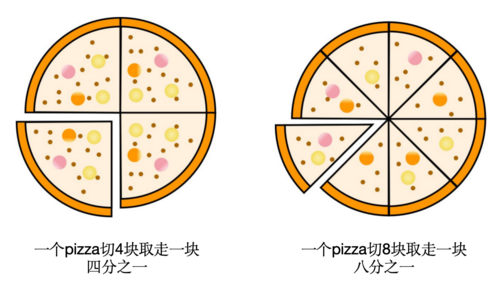
另外，当我们谈论分数的时候，经常会说到几分之一，几分之一的含义就是:把一个整体分成了几个部分，取其中的一个部分就被称作几分之一。更一般地，几分之几的含义就是:把一个整体分成了分母数值那么多个部分，取其中的分子数值那么个部分，这两个数一般不同，就被称作几分之几^[1]。(图片来源于《小学数学这样学》^[1])

这里，其实就是化归的思想在指导着我们在这样思考，顺着分数(新概念新知识)的含义，把新的知识化归到已经学会的知识上，从而在学会新概念的基础上又不增加我们的学习负担，看，化归的思想威力多大！

值得注意的是，分数的分母不能是零，直接来源就是除数是零的时候，因为除法就是重复的减法，也就是减法的简便运算，重复减去零，看能减几次的时候，你会发现永远都减不完，这时候就会直接进入一个你现在很难处理的数学对象，无穷大。于是在这个阶段，我们不讨论这个情况。

带分数

带分数，指的是，当分数的值大于1时，直接可以写成整数 [math]\displaystyle{ + }[/math] 分数 的形式，其中整数部分是大于1的部分，分数部分是小于1的部分^[1]。

例如， [math]\displaystyle{ 1+\frac{1}{2}=\frac{3}{2} }[/math] 可以写成 [math]\displaystyle{ 1\frac{1}{2} }[/math]^[1]。

而[math]\displaystyle{ 1\frac{1}{2} }[/math]，这样的形式，有时候，也有人称之为假分数。但是，进行这样的很细致的分类我们不建议，因为没有新增什么有用的信息。我们在这里提一下这个概念，只是让你知道有这个东西，防止以后有人提起这个概念你不明白他们在说什么，仅此而已。

因为，在你真的很熟悉分数的含义以后，带分数的概念也是可以没有的，只需要理解了分数就可以涵盖像带分数、假分数这些概念。我们坚持用更少的概念帮助你建立数学学科的大厦，相信我们，这样你的记忆负担会更少，而且建立起来的数学大厦也会更稳固。

乘法和除法的统一

从分数的定义出发， [math]\displaystyle{ \frac{1}{2} }[/math] 就是把一个整体分成了两份，取出其中的一份。如果这时候我问： [math]\displaystyle{ 4 \times \frac{1}{2} }[/math] 等于多少，这时候借助乘法是重复的加法的定义，我们把4个 [math]\displaystyle{ \frac{1}{2} }[/math] 加起来，发现是2。这和 [math]\displaystyle{ 4 \div 2 }[/math] 得到的结果是相同的^[1]。

这时候，我们从运算来验证一下。因为分数线就是除号，所以我们有[math]\displaystyle{ 4 \times \frac{1}{2} = 4 \times 1 \div 2=2 }[/math]，结果没问题。

所以，我们更进一步归纳，把把4和2替换成任何整数，因此，一般地我们有:一个数除以一个整数，等于，前一个数乘上后一个整数的倒数^[1]。也就是， [math]\displaystyle{ a \div b=a \times \frac{1}{b} }[/math] 。

但是我们不满足于在整数范围内讨论，于是我们继续问： [math]\displaystyle{ 4 \div \frac{1}{2} }[/math] 等于多少？依据分数的含义和定义，我们给这个数学关系找一个对应的例子：有四个馅饼，把每一个馅饼切成 [math]\displaystyle{ \frac{1}{2} }[/math] ，请问最后一共有多少块 [math]\displaystyle{ \frac{1}{2} }[/math] 的馅饼？如果我们实际切一下，然后数一数，就发现有8块。于是我们得到[math]\displaystyle{ 4 \div \frac{1}{2} =8 }[/math]。

我们从运算来验证一下，

其中， [math]\displaystyle{ (1 \div \frac{1}{2}) }[/math] 代表着把每一个馅饼切成 [math]\displaystyle{ \frac{1}{2} }[/math]。于是你就看到和上面我们例子中可以一一对应的部分了。试一试自己想明白吧。

这时候，我们使用代数的思想来总结， 有[math]\displaystyle{ a \div \frac{b}{c}=a \div b \times c=a \times \frac{1}{b} \times c = a \times \frac{c}{b} }[/math] ，也就是一个数除以一个分数，就是前一个数乘上后一个分数的倒数。

于是，我们在分数、倒数的基础上，看到了乘法和除法的统一。顺便，我们还通过负数看到的加法和减法的统一。化归的思想在发挥着作用，数学的魅力开始展现。

分数的性质

分数的性质，指的是，分子分母同时乘以(或者除以)一个非零的数，分数值不变^[1]。

本质上，这是由于分数的含义导致的。从分数的含义我们知道，分数线可以看作是除号，于是一个分数就可以写成除法的形式，下面举一个例子：

鼓励你一定要仔细思考并理解其中的每一步。提示：这里用到了运算律的知识。当你明白了这个性质以后，就打开了进一步使用分数的大门。鼓励你在使用中细细体会和品味这个性质的重要性。

分数的运算

我们从分数的含义出发，也就是分数线就是除号，于是我们就把分数变成了在整数上的除法，于是就自然连接到了我们已经学会的四则运算上了。

但是，有了这层分数的含义，我们还不能很好的完成分数的运算。因为我们虽然在理论上已经可以通过四则运算来完成分数的四则运算，但是在具体操作上仍然存在问题，因为你不能把几个分数都用除法一直算算算，然后再把这些分数的值进行加减乘除，因为这只是从分数的运算变成小数的运算，而且如果遇到无限小数，那么这是一件很难完成的事情。

于是我们又要回到分数的含义思考。我们还可以把分数看作是一个整体的一部分。从这里出发，我们发现，要做分数的加法，如果两个分数的分母是一样的，那么就相当于从同一个整体中取出来一部分和另一部分合起来数一数，看看占总体的多少。于是这两个分数的分子就是同一个整体中的两个部分，加法就是把这两部分合起来数一数，于是分子就是直接相加。我们想要的是，得到的合起来数一数的数量占总体的多少，而总体就是它们相同的分母，于是就是分子相加起来的数除以分母。于是我们就有了分数的加法的原理：如果两个分数的分母相同，那么两个分数相加，就是分子相加，分母不变。

其实，我们还可以从运算的角度来看^[1]，例如:

所以问题的关键就在于，如何去把任意两个分数变成分母相同的两个分数。这里我们思考一下分数的性质。我们是不是可以让两个分数的分母分别乘上不同的数使得它们变成相同的数，为了不改变分数的值，从分数的性质出发，我们也对分子乘上相同的数。

那么问题又来了，如何确定两个不同的分母分别该乘上多少才能让两个分母相等呢？从公倍数的角度思考一下。于是，我们把这个寻找不同分数的相同分母的过程，称之为通分。

约分是与通分相对的操作，其本质也是利用了分数的性质。为了分数的统一表达，使得我们能够更容易看出来不同分数的关系，或者是为了使得分数参加的运算更加简单，我们会需要经常把分数写成最简分数，也就是利用分数的性质，把分子和分母变成两个没有公因数的数，于是我们把这个过程称之为约分。

为什么这里我们只研究了加法？因为四则运算本质上都可以回到加法，于是其他运算都可以通过加法来实现。至少减法是很容易这样想明白的。至于分数的乘法和除法，直接利用分数的含义，分数线就是除号，就可以转换为整数的四则运算，最后又可以把结果返回到分数的形式上。

分数和小数的关系

我们可以从数轴上分割刻度的例子，很自然想到了分数，因为分数的含义，就是将一个整体平均分。

所以从数轴的角度来说，分数和小数似乎天然就是有联系的，按照把1份2到3的整数的间隔刻度分成10份，上面的 [math]\displaystyle{ 0.1 }[/math] 也可以写成分数 [math]\displaystyle{ \frac{1}{10} }[/math] 。

另外，你还可以从运算层面感受一下这个自然的过程，有了小数的基本定义后，从分数到小数是很自然的，不信你去试一试 [math]\displaystyle{ \frac{3}{7} }[/math] 等于多少？(提示：根据分数的含义，分数线就是除号，于是分数在运算上自然就是除法)。无论能否除尽，反正它会是一个小数。

下面可以给出一个证明，证明分数是可以表示成有限小数或者是无限循环小数的，看不懂也没关系：

考虑分数[math]\displaystyle{ \frac{m}{n} }[/math]，m＜n。如果这个分数能化为有限小数，结论成立。如果不能化为有限小数，用m除以n必有余数，显然，这个余数只能取1和n-1之间的一个整数。根据除法的运算法则，有余数后的除法需要用0填位。因此，最多n次运算后，某个余数必然还要出现第二次，并且在以后的运算中周期出现，这就形成了循环小数。这就证明了：所有的分数都可以化为有限小数或者无限循环小数^[2]。

有限小数到分数，是非常简单的，由于进制系统，小数的小数部分的数位可以用平均切分一个数位上的值为10份来表示，这是你已经知道的事情，下面我们详细举例说明，例如 [math]\displaystyle{ 0.1 }[/math] 就等于 [math]\displaystyle{ \frac{1}{10} }[/math]。所以 [math]\displaystyle{ 0.2 }[/math] 就等于两份的[math]\displaystyle{ \frac{1}{10} }[/math]， [math]\displaystyle{ 0.12 }[/math] 就等于12份的 [math]\displaystyle{ \frac{1}{100} }[/math] 。

照此使用代数的思想，我们很容易得到可以推广到任意有限小数都可以和分数互相表示的结论。

那么无限小数呢？无限小数中的无限循环小数，可以通过运算来说明白，这也是一个证明过程：

这里我们是随便举了个例子，你可以使用代数来重新证明一遍，然后就可以推广到全部的无限循环小数了。

那么无限不循环小数和分数能否互相表示呢？答案是不能。于是产生了无理数。

于是我们有结论：所有的分数都可以表示为小数，这些数是有理数。无限不循环小数不能表示为分数，这些数是无理数。

最简分数

最简分数，指的是，分子分母都是质数的分数。这个时候，最简分数不能再使用约分来进行简化。

值得注意的是，一般来说，当你需要研究分数的结构或者讨论分数的性质的时候，把它化简最简分数一般都会有助于你去更进一步思考这个分数的性质和结构。但是，并不是任何时候都需要把分数化简，有时候，例如不同分数相加减的时候，我们还需要把最简分数进行通分，寻找它们的最小公倍数。所以，这里要告诉你的是，在进行任何一个操作之前，你需要问一问自己为什么要进行这个操作，因为任何一个操作其实都需要对应着一个明确的目的，这样的思考方式希望你迁移到任何一件事情的思考上去。