定义和含义

三角形，指的是，由三条不同的线段首尾相连构成的图形^[1]。

构成三角形的三条线段分别称为三角形的三条边，其两两相交构成的三个角称为三角形的内角。

(图片来源于《小学数学这样学》^[1])

层次标注

在这里，它属于第二层知识，即学科概念。

辅助理解的解释

三角形，顾名思义，也就是有三个角和三条边的封闭图形。三角形是最简单的多边形，因为构成一个多边形至少需要三条线段。

正因如此，很多复杂的多边形都可以被分割为多个三角形来研究，将一个多边形问题化归为三角形问题。因此如果想要认真研究平面几何，就必须对三角形有足够的理解。

三角形内部变量

三角形的内部变量有三个边长和三个角度(也就是三角形的三个内角)。这是我们研究三角形主要关注的对象。

一般的，分析一个研究问题中有多少个变量，是很重要的一步，能够帮助我们建立数学模型来求解问题。

这部分内容摘自《小学数学这样学》^[1]。

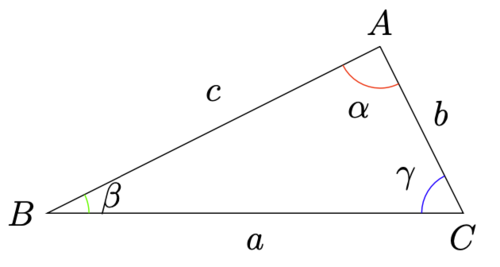
我们先来定义几个和三角形有关的量。三条线段称为三角形的三条边。 例如，图中的[math]\displaystyle{ \overline{A B} }[/math]、 [math]\displaystyle{ \overline{B C} }[/math] 、 [math]\displaystyle{ \overline{C A} }[/math] 。有的时候也把边记作相应的对顶点的字母的小写字母，例如图中的[math]\displaystyle{ a }[/math] 、 [math]\displaystyle{ b }[/math] 、 [math]\displaystyle{ c }[/math] 。其长度就称为三角形的边长。三个夹角称为三角形的三个内角, 例如图中的 [math]\displaystyle{ \angle A B C }[/math] 、 [math]\displaystyle{ \angle B C A }[/math] 、 [math]\displaystyle{ \angle C A B }[/math] 。 有的时候也给内角专门的记号, 例如图中的 [math]\displaystyle{ \angle \alpha }[/math] 、 [math]\displaystyle{ \angle \beta }[/math] 、 [math]\displaystyle{ \angle \gamma }[/math] 。

边和角, 以及相应的边长和角度, 是一个三角形最基本的内部属性。原则上，只有这六样东西都对应相等，两个三角形才能看作一模一样的三角形。也就是说， 一个三角形就意味着 [math]\displaystyle{ \triangle(a, b, c, \alpha, \beta, \gamma) }[/math] , 六个内部变量决定一个三角形。不过，我们稍后就会发现其实不用这六样东西都对应相等，两个三角形就可以认为是一模一样的，是全等的。

三角形的面积

在有了平行四边形的面积之后，我们就可以来计算一般的三角形的面积了。

割补的方式求三角形面积

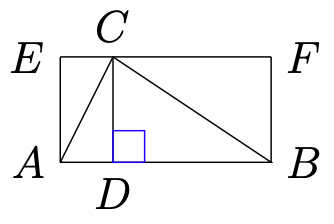
首先最简单的方法是割补，下面我们来从三角形割补为一个长方形，如图(三角形求面积(长方形割补))所示。

我们先在一条底边上作一个高。沿着高把高左边和右边的三角形各自复制一份，翻上去，补充到这两个三角形上面。我们会得到一个长方形，如上图所示，其边长分别是三角形的底边的长度和高的长度。于是，我们得到三角形的面积就是这个长方形面积的一半，也就是：

[math]\displaystyle{ S=\frac{1}{2} \times a \times h }[/math]，其中a是底，h是与a这条底相配套的高。注意，a和h是配套的，高必须是对应的底边上的高。

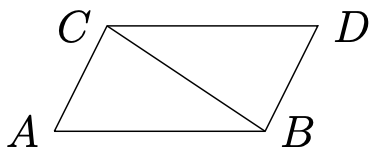
然后，我们从另一种方式来继续使用割补，我们下面来从一个平行四边形割补为两个三角形，如图(三角形求面积)所示。

我们将平行四边形沿着点C和点B连一条线段[math]\displaystyle{ \overline{C B} }[/math](我们称这条线段是对角线，因为角[math]\displaystyle{ \angle ACD }[/math]和角[math]\displaystyle{ \angle ABD }[/math]分别是两个相对的角)。然后我们可以通过三角形全等判定定理来证明由对角线分割出来的两个三角形全等。所以三角形的面积其实就是这个平行四边形面积的一半，而我们沿着点C作三角形的高，发现这条高既是三角形的高又是平行四边形的高，而它们俩又是共同的同一条底。

所以在这基础上，我们发现，通过平行四边形的面积是底乘以高，我们就知道了三角形的面积是底乘以高除以二，也就是：

其中a是底，h是与a这条底相配套的高。 注意，底和高要配套，一定要保证这条高就是选择的底边上的高。三角形的每一条底边上都有一条高。它们的长度不一定相同^[1]。

等差数列求和的方式求三角形面积

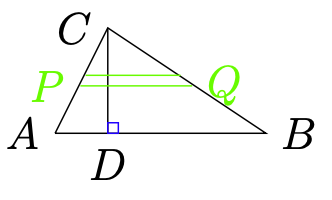
学会了等差数列后，我们把三角形的一条底边平行地在三角形内来划线，把三角形分成很多很多条带有一定厚度的底边。例如我们要求厚度刚好就是一个标准单位。例如，如果高是100厘米，我们就把每一条和底边平行的三角形内的条带的厚度设成1厘米。就好像是下图中的P,Q之间的条带^[1]，如图(三角形求面积(等差数列))所示。

这样，我们发现，刚好需要在三角形内分出来[math]\displaystyle{ 100 \div 1 }[/math]这么多条厚度为1的条带。这些个条带的长度构成一个等差序列:最大值是原来三角形底边的长度，最小值就是0，这样的条带有高的长度这么多条。于是，按照等差序列的求和的方法，把最大值(底边长度)和最小值(0)加起来除以2，然后乘以这些数的个数，我们同样得到三角形的面积公式，底乘以高除以二，也就是：

其中a是底，h是与a这条底相配套的高。

至于为什么这些线段的长度构成的就是一个等差序列，需要通过证明(需要三角函数的知识)来回答。不过，即便现在暂时不会这个证明，也没关系，因为我们知道这些由画出来的线段和原来的顶点构成的三角形的形状都是一样的，因此，高越长，对应的底边肯定越长，而且，这个长度的增加是等比例的。这里我们用到了平行线的性质——通过平行线在三角形里面划分出来的小三角形和整体的三角形相似(由于每一个角的度数都不变，而平行线相应的角相同属于平行线的性质)，以及相似图形的性质——相似三角形每一条边对应成正比，所以每一个划分出来的三角形的底边的长度必定和那个三角形上的相应底边上的高的比值相同。于是，把高分成等差序列，就意味着把底边也分成等差序列^[1]。

不过，就算我们不通过这个等差序列的求和来推导三角形的面积公式，通过割补还有运用长方形，平行四边形，我们也得到了三角形的面积公式^[1]。

这个等差序列的计算方法包含了一个叫作积分的重要思想。将来我们会再次用到^[1]。

附，"这些线段的长度构成的就是一个等差序列的证明，基于三角函数"，这部分内容摘自《小学数学这样学》^[1]。：

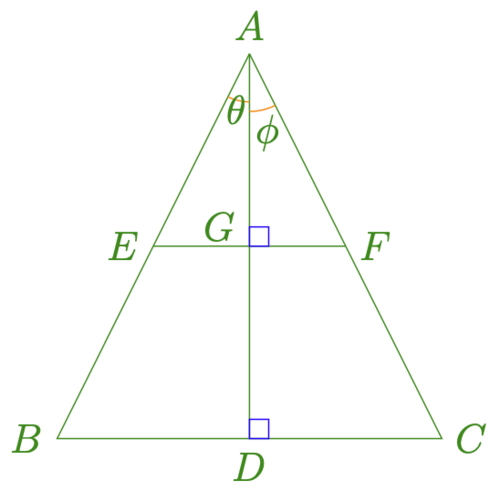
如图(三角形内平行底边的线段的长度)所示，我们通过高和角[math]\displaystyle{ \theta }[/math]的正弦函数和余弦函数(三角函数)来计算三角形内平行于底边的线段的长度。通过这个计算，我们来证明，只要每一条线段把高均匀切分，则这个线段的长度也是均匀增加的，也就是构成一个等差序列。

我们来算一下线段EF的长度。为了计算EF我们先来看看EG和θ角以及AG的关系:

同理，右侧，

合起来，

也就是说，EF的长度和AG的长度一一对应，后面的不过就是一个常数。于是，只要我们切分高的时候均匀切分，EF的长度也是从底边长度BC均匀地缩小成0。也就是说，各个平行于底边的线段的长度构成一个等差序列。