定义和含义

三角形内角和等于180度公理，指的是，三角形内角和等于[math]\displaystyle{ 180^{\circ} }[/math]^[1]。

也就是说，对于任何三角形 [math]\displaystyle{ \triangle A B C }[/math] , 其内角和可以表示为:[math]\displaystyle{ \angle A+\angle B+\angle C=180^{\circ} }[/math]。

(图片来源于《小学数学这样学》^[1])

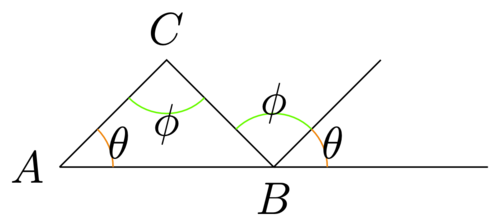
如果你学习了平行公理以及平行线的性质定理，我们会发现，图(三角形内角和等于180度的展示)中标示相同的角相等，于是三角形的三个内角加起来就相当于一个平角^[1]。

层次标注

在这里，它属于第二层知识，即学科概念。

辅助理解的解释

这是一条非常重要的定理，甚至你可以把它当作一条公理。

当它是一条公理时，从它出发可以推出平行公理。当然，如果从距离公理出发，加上三角函数的知识，你可以推导出三角形内角和等于[math]\displaystyle{ 180^{\circ} }[/math]，这时候它就是一条定理。

你需要明白，如果从生活中剪下大量的三角形来测量进而得到三角形内角和等于[math]\displaystyle{ 180^{\circ} }[/math]这个结论，是不可靠的。数学上，一定要依靠证明来帮助你更进一步思考，只有经过正确推理证明的结论才是可靠的，你可以用测量等方式来验证你的推理证明的结论是否正确，但是不能把测量得到结论当作一个能够作为更进一步思考的基石。这在数学中是很重要的。

从三角形内角和公理到平行线唯一性公理

这个证明基于三角形内角和公理、直角三角形锐角可以取任意小定理、直角三角形长边对大角引理。

(图片来源于《小学数学这样学》^[1])

以下是摘自《小学数学这样学》的证明内容^[1]：

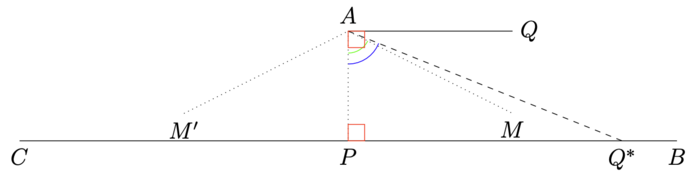
证明：如右图(从三角形内角和公理到平行公理)所示，我们先来作一条过直线外一点 [math]\displaystyle{ A }[/math] 平行于 [math]\displaystyle{ B C }[/math] 的平行线: 先作过直线外一点 [math]\displaystyle{ A }[/math] 的 [math]\displaystyle{ B C }[/math] 的垂线，垂线和 [math]\displaystyle{ B C }[/math] 的交点记作 [math]\displaystyle{ P }[/math] ; 然 后, 我们再来作一条过直线上一点 [math]\displaystyle{ A }[/math] 垂直于 [math]\displaystyle{ A P }[/math] 的直线 [math]\displaystyle{ A Q }[/math] 。

有了这个图，我们来证明 [math]\displaystyle{ A Q \| C B }[/math] 。由于 [math]\displaystyle{ \angle A P B }[/math] 和 [math]\displaystyle{ \angle P A Q }[/math] 都是直角, 因此, 两者互补。对于直线 [math]\displaystyle{ A Q }[/math] 和 [math]\displaystyle{ C B }[/math] 而言, 这两个角度刚好就是同旁内角。同旁内角互补, 则直线平行。我们得到 [math]\displaystyle{ A Q \parallel C B }[/math] 。

现在，我们假设平行公理不成立，也就是说过直线外一点要么不存在 (已经被上面的作图过程否定) 任何一条平行线, 要么存在两条或者两条以上的平行线。现在，我们来证明存在两条平行线也是不可能的。 证明两条的情况以后, 两条以上就可以自然被否定。记这个第二条平行线为 [math]\displaystyle{ l }[/math] ——过 [math]\displaystyle{ A }[/math] 点, 指向不同于 [math]\displaystyle{ A Q }[/math] 的一条直线。

我们说, [math]\displaystyle{ l }[/math] 要么是图中左侧往下 [math]\displaystyle{ A M^{\prime} }[/math] 的方向, 要么是图中右侧往下 [math]\displaystyle{ A M }[/math] 的方向。如果既不是左侧往下，也不是右侧往下，则只能和 [math]\displaystyle{ A P }[/math] 垂直，也就是 [math]\displaystyle{ \angle P A M=\angle P A Q=90^{\circ} }[/math] 。于是，根据过直线上一点有且只有一条垂线, [math]\displaystyle{ l }[/math] 就是 [math]\displaystyle{ A Q }[/math] 。矛盾。也就是说 [math]\displaystyle{ \angle P A M \neq \angle P A Q= 90^{\circ} }[/math] 。

我们取出来其中一种情形 [math]\displaystyle{ A M }[/math] 来讨论。[math]\displaystyle{ A M^{\prime} }[/math] 的情形类似。注意, [math]\displaystyle{ A M \| C B }[/math] , 因此, [math]\displaystyle{ A M }[/math] 和 [math]\displaystyle{ C B }[/math] 没有交点。同时, 由于 [math]\displaystyle{ A M }[/math] 在右侧往下, 因此, [math]\displaystyle{ \angle P A M\lt \angle P A Q }[/math] (如果大于, 就自然成了 [math]\displaystyle{ A M^{\prime} }[/math] 的情形)。

根据直角三角形锐角可以取任意小定理, 当 [math]\displaystyle{ \angle P A M\lt \angle P A Q }[/math] 的时候, 我们总是可以找到一个直角三角形 [math]\displaystyle{ \triangle A P Q^{*} }[/math] ，其中 [math]\displaystyle{ Q^{*} }[/math] 在直线 [math]\displaystyle{ C B }[/math] 上)，使得 [math]\displaystyle{ \angle P A M\lt \angle P A Q^{*} }[/math] , 或者说反过来, 使得 [math]\displaystyle{ \angle Q A Q^{*}\lt \angle Q A M }[/math] 。

根据直角三角形长边对大角引理，我们知道小角对小边，也就是 [math]\displaystyle{ A M }[/math] 必定交 [math]\displaystyle{ B C }[/math] 于一点，而且这个点在 [math]\displaystyle{ P Q^{*} }[/math] 的内侧。这个结论和 [math]\displaystyle{ A M }[/math] 平行于 [math]\displaystyle{ B C }[/math] 矛盾。

因此，原假设错误，也就是过直线外一点 [math]\displaystyle{ A }[/math] 有且只有一条平行于 [math]\displaystyle{ B C }[/math] 的直线。