分类:圆
朴素定义和含义
圆,朴素来说,指的是,一个平面上各个点到中间那个点的距离都一样的图形[1]。
定义和含义
圆,指的是,到某个给定点[math]\displaystyle{ (P) }[/math]距离相同(距离取值可以是一个任意值[math]\displaystyle{ r }[/math])的点的集合称为圆,也就是:
其中,[math]\displaystyle{ P }[/math]称为这个圆的圆心,[math]\displaystyle{ r }[/math]称为这个圆的半径。
层次标注
在这里,它属于第二层知识,即学科概念。
辅助理解的解释
圆的两个要素是:圆心(中心点)和半径[math]\displaystyle{ (r) }[/math]。
中心点移动不改变面积、周长,因此,圆的形状实际上只由半径[math]\displaystyle{ (r) }[/math]这一个变量决定,也就是[math]\displaystyle{ C=f(r) }[/math]和[math]\displaystyle{ S=g(r) }[/math][1]。这里用到了量纲分析。
从圆的周长得到圆周率
由于周长的单位是长度单位,而圆的半径的单位也是长度单位,所以圆的周长理论上来说,就是一个未知的常数乘上半径,可以写为:[math]\displaystyle{ C = 常数\Pi \times R }[/math],这里[math]\displaystyle{ R }[/math]是半径。
目前,我可以直接告诉你,这个常数[math]\displaystyle{ \Pi }[/math]是圆周率的2倍,大约等于6.28。
但是,这个数是怎么来的呢?
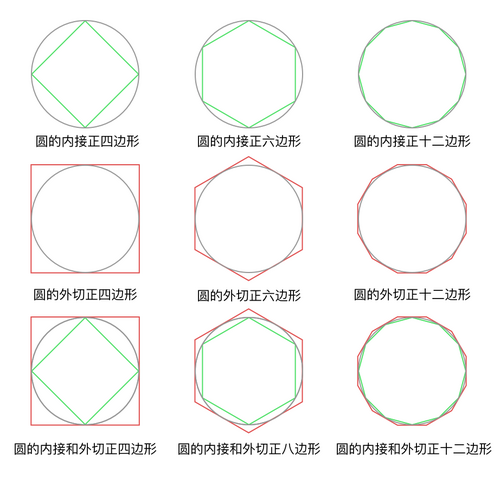
我们来看两个和圆相关的概念,圆的内接多边形和圆的外切多边形。
圆的内接正多边形,指的是,一个正多边形的所有顶点正好都在圆上,这样的正多边形我们称为圆的内接正多边形。
圆的外接正多边形,指的是,一个正多边形的所有边都正好和圆相切。这里所谓的相切,就是多边形的一条边和圆正好只有一个交点。这样的正多边形我们称为圆的外切正多边形。
我们可以从图中直观的看到,对于同一个圆来说(我们假设这四个圆是一样大的),随着正多边形的边数增加,外切正多边形的周长在逐渐缩小以靠近圆的周长,与此同时,内接正多边形的周长在逐渐增加以靠近圆的周长。这时候,如果我们继续思考,如果这两个正多边形的周长不断增加,那么中间留给圆的周长的部分也就越来越小,似乎就是用两个正多边形的周长就可以把圆的周长夹在中间挤压,最后这两个正多边形的周长都会非常靠近圆的周长,这样就可以把圆的周长大致确定下来了。
也就是说,
这里,我们有4组数据,是已经算好了的。(至于怎么算,如果你学了三角函数后,你可以借助计算器来算任意边数的正多边形的周长。在这里,如果你会勾股定理,那么你可以算一下当内接和外切的都是正四边形时的情况。另外,你可以用外切正六边形和内接正六边形算一下看看,因为正六边形是特殊的正多边形,如果你把圆心和各个顶点连起来后,你会发现正三角形,而正三角形是三边全等的三角形,而这里面的斜边和邻边以及对边的比值,你可以通过查表得到,如果没有表,也可以去使用计算器来帮助你。)
当内接和外切的都是正四边形时:[math]\displaystyle{ 5.656r \lt 圆的周长 \lt 8r }[/math] ,也就是 [math]\displaystyle{ 5.656 \lt \Pi \lt 8 }[/math]
当内接和外切的都是正六边形时:[math]\displaystyle{ 6 \lt \Pi \lt 6.928 }[/math]
当内接和外切的都是正十二边形时:[math]\displaystyle{ 6.212 \lt \Pi \lt 6.431 }[/math]
当内接和外切的都是正二十四边形时:[math]\displaystyle{ 6.265 \lt \Pi \lt 6.319 }[/math]
这时候,你是不是就能看到圆的周长随着内接和外切的正多边形的边数增加,范围越来越小,似乎是越来越可以有一个差不多能够用来估计的值了。还记得在上面,我告诉过你,圆的周长大约是半径的6.28倍吗?
这里,这样两头向中间挤压的来估计一个未知数的值的思维方式,叫作夹逼的思想。另外,通过不断去增加参数的值,最后甚至是用脑袋去思考如果一直增加下去的会怎么样的思维方式,叫作极限的思想。
以后试着再其他问题上体会一下这两个思想。
为了统一符号,我们记这个常数[math]\displaystyle{ \Pi }[/math]为[math]\displaystyle{ 2\pi }[/math],并且在计算中用[math]\displaystyle{ \pi \approx 3.14 }[/math],于是我们有圆的周长和半径的关系是[1]:
而这里的[math]\displaystyle{ \pi }[/math],就是圆周率。
从圆的周长到圆的面积
接着上面的,中心点移动不改变面积、周长,因此,圆的形状实际上只由半径[math]\displaystyle{ (r) }[/math]这一个变量决定,[math]\displaystyle{ S=g(r) }[/math]。
从量纲定理出发,因为半径的单位是长度单位,而面积的单位是长度单位的平方,所以圆的面积肯定是某个常数乘上半径的平方,也就是[math]\displaystyle{ S~R^2 }[/math]。现在我们来找出这个常数。
我们现在给定一个半径为[math]\displaystyle{ R }[/math]的圆,它的周长就是[math]\displaystyle{ 2 \pi R }[/math]。
从等差数列的角度求圆的面积
现在,我们先从等差数列的角度来计算圆的面积。下面内容取自《小学数学这样学》[1]。
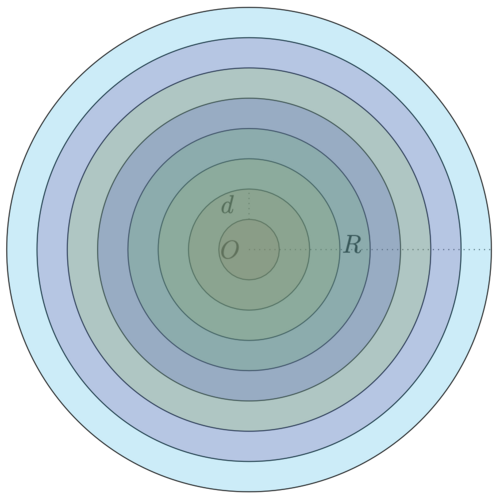
(图片来源于《小学数学这样学》[1])
圆的周长随着半径变短不断地减小。也就是说,如果我们在上面给定的圆内不断地画出圆环,其半径从[math]\displaystyle{ r = R }[/math],每次取一个间隔[math]\displaystyle{ d }[/math],一直到[math]\displaystyle{ r=0 }[/math],我们就可以铺满整个圆,
如图所示,这时候,[math]\displaystyle{ r }[/math]从[math]\displaystyle{ R }[/math]变成了0。每一步这样的圆的周长就是[math]\displaystyle{ 2\pi r }[/math],每个圆环的面积是[math]\displaystyle{ 2\pi rd }[/math]。我们可以把这样的周长排成一个三角形,也就是一个等差序列:从[math]\displaystyle{ 2 \pi R }[/math]慢慢地变成0。对于这个三角形,我们只需要知道这个三角形的高就可以算出来这个三角形的面积。我们说,这个三角形的高度就是[math]\displaystyle{ R }[/math]。于是,面积就是:
那为什么我们说这个三角形的高度就是[math]\displaystyle{ R }[/math]呢?因为看正中间的水平半径,我们可以发现,半径,也就是相当于变换以后的三角形的高的范围,正好就是从[math]\displaystyle{ R }[/math]到0。
用带有具体数的例子来说,对于一个半径R就是比如说100厘米的圆,试想你用一层层厚度固定但是厚度比较小例如1厘米的圆环来填满这个圆。你觉得需要多少个这样的圆环来填满?肯定就是[math]\displaystyle{ 100 \div 1 = 100 }[/math]个这样的圆环。也就是,对于半径为[math]\displaystyle{ R }[/math]的圆,我们以一个个厚度为一个标准单位的圆环来填满这个圆,我们刚好需要R个这样的圆环。每一个圆环上的面积,刚好就是圆环的周长乘以这个厚度单位。于是,每一圈的面积刚好就是[math]\displaystyle{ 2 \pi r }[/math],而且我们需要R个这样的圆周线。转化为三角形的语言,我们的底边长度的范围是从[math]\displaystyle{ c=0 }[/math]到[math]\displaystyle{ c = 2 \pi R }[/math],每一条的面积是[math]\displaystyle{ c }[/math],这样的底边有[math]\displaystyle{ R }[/math]条。这样就给出来了一个底边长度为[math]\displaystyle{ 2 \pi R }[/math],高为[math]\displaystyle{ R }[/math],每一层的厚度就是一个单位长度的三角形。这个三角形的面积就是底乘以高除以2,也就是[math]\displaystyle{ \pi R^2 }[/math]。
我们还可以更加严格一点来计算。我们每一圈的圆环的宽度为[math]\displaystyle{ d }[/math],那么,我们需要多少个这样的圆环才能填满这个圆呢?答案是:[math]\displaystyle{ N = \frac{R}{d} }[/math]
那么,我们就相当于要计算如下算式,
这个结果和我们给的答案[math]\displaystyle{ S= \pi R^2 }[/math]相差了一点点,[math]\displaystyle{ πR \times d }[/math]。但是,你要注意,这里的[math]\displaystyle{ d }[/math]我们可以要多么小就多么小,也就是把每个小圆环分的窄一点。因此,给定了[math]\displaystyle{ R }[/math]之后,第一项[math]\displaystyle{ \pi R^2 }[/math]一个确定的值,但是第二项[math]\displaystyle{ \pi R \times d }[/math]是一个要多小就可以多小的值。于是,我们说第二项可以忽略。
通过把一个几何图形切分成一条一条,然后把这个一条一条看作三角形、长方形等已经知道如何计算面积的多边形来计算几何图形的面积,是一个非常重要的思想,是积分思想的雏形。
从割补的角度求圆的面积
下面的内容取自《小学数学这样学》[1]。
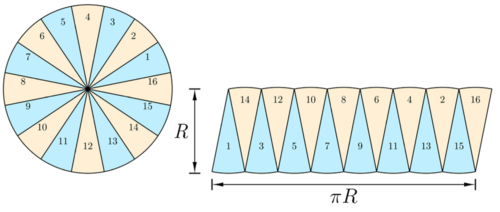
把圆周切成很多个等份,每一个切分的点都和圆心连起来,沿着这些半径连线剪开,不要剪断圆周,再把圆周展开拉平可以得到一个锯齿状的图形,如图所示。
(图片来源于《小学数学这样学》[1])
可以发现,这个图形就是一个个的三角形。每一个三角形的面积都是底乘以高除以2,所以合起来就是圆的周长乘以高除以2。只要这个高就是[math]\displaystyle{ R }[/math],我们还是得到同样的算式,[math]\displaystyle{ S=\frac{1}{2} 2 \pi R \times R=\pi R^{2} }[/math]。至于为什么这个高就刚好是[math]\displaystyle{ R }[/math],大概可以这样来想象一下,注意是想象不是严格的证明:每一个三角形都是一个等腰三角形,腰的长度就是[math]\displaystyle{ R }[/math],由于每一个底边非常非常小,因此,这个三角形的高也非常非常接近腰的长度。