分类:勾股定理
定义和含义
勾股定理,或者是Pythagoras定理,指的是,如果平面上直角三角形的两条直角边的长度记为[math]\displaystyle{ a }[/math]和[math]\displaystyle{ b }[/math],斜边的长度记为[math]\displaystyle{ c }[/math],则有[math]\displaystyle{ c^{2}=a^{2}+b^{2} }[/math][1]。
这看似简单的一条定理,其实背后隐藏着一条深刻的公理,也就是距离公式公理。二者在平面直角坐标系中,是等价的。
层次标注
在这里,它属于第二层知识,即学科概念。
使用量纲定理来证明勾股定理
这部分如果不明白,没关系,我们还有割补的证明的方法,你只要记住勾股定理的含义就行,因为这其实是就是距离公式公理。
这是来自Albert Einstein的证明,这部分内容摘自《小学数学这样学》[1],具体如下:
(图片来源于《小学数学这样学》[1])
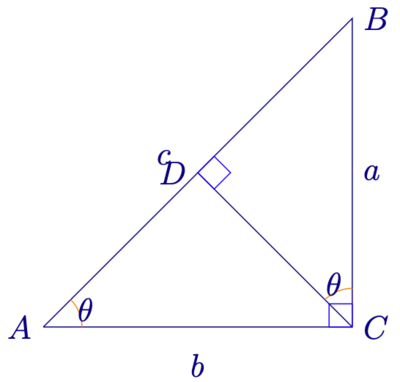
对于直角三角形来说,其形状由两个因素决定,要么就是两条直角边的长度,要么就是斜边的长度和一条直角边的长度,要么就是斜边的长度和斜边与一条直角边的夹角。
每一个上面的条件决定了一个直角三角形这一点,我们可以通过作图来验证。为了下面的证明方便,我们取斜边的长度[math]\displaystyle{ c }[/math]和斜边与一条直角边的夹角[math]\displaystyle{ \theta }[/math]当作直角三角形的形状的决定因素。
于是,我们知道,直角三角形的面积,尽管我们还不会计算,肯定是[math]\displaystyle{ S = s(c, \theta) }[/math]。其中,我们知道,[math]\displaystyle{ c }[/math]的单位是长度的单位,例如米; [math]\displaystyle{ S }[/math]的单位是面积的单位,例如平方米。按照单位可计算的原则,我们可以知道,[math]\displaystyle{ S }[/math]和[math]\displaystyle{ c }[/math]之间的关系肯定是:[math]\displaystyle{ S = \lambda (\theta)c^2 }[/math]。注意,这里角度[math]\displaystyle{ \theta }[/math]就是一个数,没有单位。
于是,我们在这个直角三角形里面,作一条斜边上的高CD,可以把这个三角形分成两个小的直角三角形[math]\displaystyle{ \bigtriangleup ACD }[/math]和[math]\displaystyle{ \bigtriangleup BCD }[/math],如图所示,其面积分别为:
这两个直角三角形合起来正好就是原来的三角形,于是面积也相同,所以:
只要[math]\displaystyle{ \lambda (theta) \ne 0 }[/math](对于需要计算面积的三角形,这个条件自然满足),等式两边同时除以[math]\displaystyle{ \lambda (theta) }[/math],就得到:
使用割补来证明勾股定理
(图片来源于《小学数学这样学》[1])
这是来自Pythagoras的证明,时间要更早一些,而且从内容来说也更容易接受一些。但是,我还是鼓励你尽量去看明白量纲定理证明,因为这是一种很重要的方法,可以迁移到很多问题。
这是具体的割补的证明,这部分内容摘自《小学数学这样学》[1]:
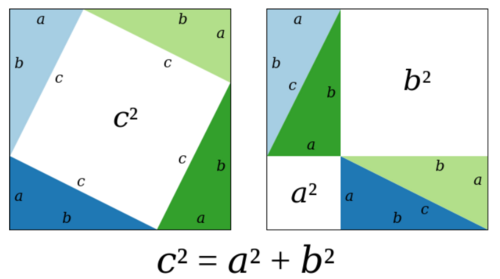
首先,把一个边长为[math]\displaystyle{ a+b }[/math]的正方形做两种不同的分割。
第一种分割是四个相同的直角三角形把边长为[math]\displaystyle{ c }[/math]的正方形围在中间。第二种分割是把四个三角形两两组合起来,剩下的是一个边长为[math]\displaystyle{ a }[/math]的正方形和一个边长为[math]\displaystyle{ b }[/math]的正方形。按照总面积不变,四个三角形的面积之和也不变,我们得到:
在这个图形切分的过程中,我们实际上用到了直角三角形的两个锐角之和等于一个直角的度数的性质,也就是三角形内角和公理[1]。也就是说,其实我们是从三角形内角和等于180度走到了勾股定理(等价于距离公式公理)。
对于一个定理来说,提出猜想固然是最重要的最具有突破性和想象力的一步,但是,严格地证明定理,也就是把这个定理建立在一个定义和公理的基础之上,或者直接当作公理的一部分,是非常重要的:只有经过这样的严格化,才能真的成为数学的形式语言体系的一部分[1]。
同时,往往经过这样的证明,就可以使得这个定理更加具有一般性,能够用于任何满足条件的问题,而不是基于具体的例子,例如"勾三股四弦五"。形式化和证明,是数学从具体情景走向一般理论的重要武器[1]。
从勾股定理到三角函数
三角函数是一类特殊的函数,角度取值连续定理,以及等差数列求解三角形面积,都是基于三角函数推导出来的。因为这部分内容又依靠了量纲定理,所以现在在小学阶段要求你来彻底理解三角函数可能很困难,不过你可以试试:
下面这部分内容摘自《小学数学这样学》[1]。
我们已经知道了直角三角形的决定变量可以取[math]\displaystyle{ c,\theta }[/math],也就是说,实际上,直角边的长度也应该是[math]\displaystyle{ c,\theta }[/math]的函数,也就是:
其中,我们再一次用了单位可计算(量纲定理)的原则。由于给定角度以后,这个[math]\displaystyle{ f(\theta) }[/math]和[math]\displaystyle{ g(\theta) }[/math]的值完全确定,我们给这两个常数(在给定[math]\displaystyle{ \theta }[/math]的条件下)一个名字,
也就是[math]\displaystyle{ sin\theta }[/math]的值是[math]\displaystyle{ \theta }[/math]对边的长度比上斜边,[math]\displaystyle{ cos \theta }[/math]的值是[math]\displaystyle{ \theta }[/math]邻边的长度比上斜边。注意,之所以能够定义这两个常数,是因为我们已经知道这两个常数的存在,也就是说,在直角三角形里面对边比上斜边得到的比例肯定和角度是对应的,也就是说,只要角度一样,就算斜边长度不一样,这个比例仍然是一样的。这个事实非常重要。有了这个事实,我们才能够定义这个角度的[math]\displaystyle{ sin }[/math]和[math]\displaystyle{ cos }[/math]的值。我们称[math]\displaystyle{ sin }[/math]为"正弦函数",称[math]\displaystyle{ cos }[/math]为"余弦函数"。
本分类目前不含有任何页面或媒体文件。