定义和含义

乘法是重复多次的加法的简便记号和简便计算。只需要理解了什么是加法（配合上理解自然数的含义，会数数），就可以理解加法如何计算，进而明白乘法是什么，乘法如何计算。

概念地图

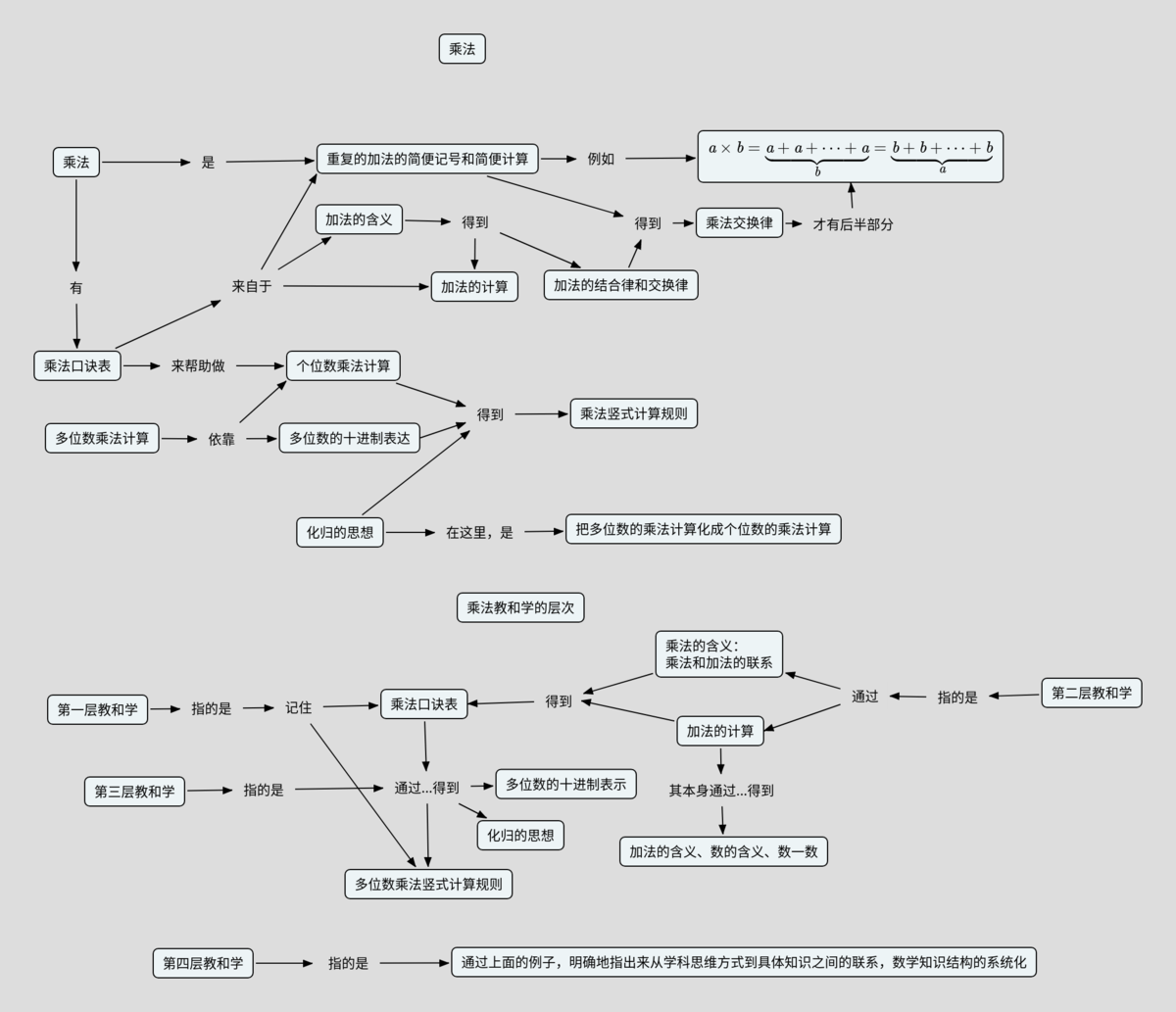
乘法的概念地图（图的格式将来改成嵌入文本的格式，用户既可以直接下载图，还可以获取这个概念地图的文本文件）：

教和学的层次

这样地直觉上通过生活经验感受到“瞬时速度”的概念的存在性，理性上相当于把动量和能量和瞬时速度联系起来，进而用极限来定义瞬时速度（计算微分的时候，不同方向的分量都要计算微分，矢量大小部分和矢量方向部分都要计算微分，每个方向的大小和方向都要计算微分），就是速度这个概念的理解型学习，属于第二层教和学。反过来，仅仅通过介绍定义，无论是平均速度和瞬时速度，都属于第一层教和学。如果进一步点出来这个从经验获得直觉，从数学获得理性，来定义和学习物理，则属于第三层和第四层教和学。

中小学阶段的理解

第一要理解到简化图的层次，也就是依赖于位置[math]\displaystyle{ \vec{x} }[/math]和时间[math]\displaystyle{ \vec{t} }[/math]来定义，暂时可以通过平均速度[math]\displaystyle{ \vec{\bar{v}} }[/math]来理解，但是要明白速度其实是一个瞬时量，称为瞬时速度，尽管不对瞬时速度的具体定义做要求。

对于学习过导数和极限的学生，可以要求理解到完整版的层次。

相对论下的含义

在相对论范畴内，速度是一个四维矢量，可以通过更加基本的物理量四维位置矢量和固有时来定义，[math]\displaystyle{ U^{a}=\frac{d X^{a}}{d\tau} }[/math]（或者用微分几何的语言定义为完全不依赖于坐标系的纯几何的形式[math]\displaystyle{ U^{a}=\left(\frac{\partial}{\partial\tau}\right)^{a} }[/math]）。其中的固有时一般不等于坐标时。如果要化成坐标时，则有[math]\displaystyle{ u^{a}=\frac{d X^{a}}{dt}\frac{dt}{d\tau} }[/math]，多出来一个因子[math]\displaystyle{ \frac{dt}{d\tau} }[/math]（尤其是其中的第一个分量[math]\displaystyle{ \frac{dx^{0}}{d\tau}=\frac{dt}{d\tau} }[/math]直接就是这个多出来的因子）。

四维位置矢量本身不依赖于坐标系，但是，在给定坐标下，四维位置矢量可以写成分量形式[math]\displaystyle{ X^{a}=[x^{0}=t,x^{1},x^{2},x^{3}]^{T} }[/math]。另外，在相对论力学范畴内，从意义上，四维动量矢量（[math]\displaystyle{ P^{a}=m U^{a} }[/math]）比四维速度矢量更容易解释：在给定坐标系下，四维动量可以看做是能量（第一分量）和三维动量（后三个分量）的结合。于是，速度的含义可以看作是，相应的动量的含义除以一个静止质量[math]\displaystyle{ m }[/math]。

量子力学下的含义

在量子力学范畴内，速度不是一个基本物理量，可以通过更基本的物理量——动量——来定义。在那里，动量和位置都成了算符，而且一般来说不对易，也就是说只能选择其中一个量的本征矢量来当做整个状态空间的基矢量。