分类:矢量
定义和含义
矢量,指的是,带有方向的数[1]。
由于我们从数轴上知道了数和点是可以一一对应的,于是矢量也是数,只不过携带了方向的信息。
矢量一般写作[math]\displaystyle{ \vec{u}=u\hat{u} }[/math],其中[math]\displaystyle{ u }[/math]是矢量[math]\displaystyle{ \vec{u} }[/math]的大小(长度),[math]\displaystyle{ \hat{u} }[/math]是矢量[math]\displaystyle{ \vec{u} }[/math]的方向。更严格的定义需要先定义矢量空间,然后矢量空间的元素就是矢量。
层次标注
在这里,它属于第二层知识,即学科概念。
辅助理解的解释
我们在数轴上知道了点和数是可以一一对应的,这里我们要告诉你其实除了一维数轴,在二维平面、三维空间,以及更高维度的空间中,矢量都是可以和那个空间的数一一对应的,而且会携带着那个空间的基本方向信息(以后你会知道,那些基本的方向信息就是单位矢量,而线段的长短信息就是这个矢量的模)。
一维数轴上的矢量
还记得加法在数轴上的表示吗?
我们说,在数轴上,加法就是加两条线段连接起来。而绘制这样的线段时,需要注意从零点画过来的方向,其实就是暗含了矢量的含义。
现在再带着矢量的含义回去看看,是否有新的理解?
对于一维矢量来说,我们用正号"[math]\displaystyle{ + }[/math]"和负号"[math]\displaystyle{ - }[/math]"来表示它的方向,用一个数来表示它的长度。例如"+2"就是一个指向正方向的长度为2的一维矢量。
二维平面中的矢量
(图片来源于《小学数学这样学》[1])
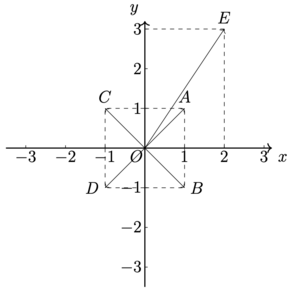
这里,在二维平面中,我们在平面直角坐标系中绘制出了几个点,我们从原点出发,分别连接了[math]\displaystyle{ A、B、C、D }[/math]四个点,记作[math]\displaystyle{ \overrightarrow{O A}, \overrightarrow{O B}, \overrightarrow{O C}, \overrightarrow{O D} }[/math],这四条头上带有方向的线段就是矢量。
在二维平面中,我们就需要两个数来表示一个矢量(对比着一维矢量来看),例如[math]\displaystyle{ \overrightarrow{O A} }[/math]相当于[math]\displaystyle{ (1,1) }[/math],也就是从[math]\displaystyle{ O }[/math]开始往[math]\displaystyle{ x }[/math]正方向走1个单位,往[math]\displaystyle{ y }[/math]正方向走1个单位,就到达了[math]\displaystyle{ A }[/math][1]。
当然,在二维平面中,我们还有另一种矢量的表示方法,稍微不太常用,也就是表示矢量的方式是给出来方向和大小。例如[math]\displaystyle{ \overrightarrow{O A} }[/math]的方向是东北方,其大小,也就是走的距离是[math]\displaystyle{ r=\sqrt{1^{2}+1^{2}}=\sqrt{2} }[/math]。在这里我们用了勾股定理来计算直角三角形的斜边的长度。合起来,我们说,矢量[math]\displaystyle{ \overrightarrow{O A} }[/math]是东北方的[math]\displaystyle{ \sqrt{2} }[/math]。
矢量加法
矢量加法,其实你在数轴上加法时就已经学过了。当时,你知道数轴上的加法就是把两个点的线段连起来。
现在,只不过我们现在要在二维的平面直角坐标系中进行,而且尝试总结出一般性的矢量加法。
在有了坐标系和矢量的含义后,我们可以来学习二维的矢量加法。我们先来看这样的图:
(图片来源于《小学数学这样学》[1])
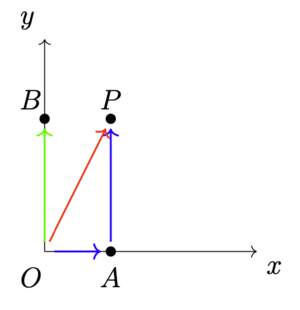
我们从原点O出发,先往[math]\displaystyle{ x }[/math]正方向走1个单位,然后往[math]\displaystyle{ y }[/math]正方向走2个单位,结合起来应该就是到达P点的位置,也就是[math]\displaystyle{ (1,2) }[/math]的位置。这个过程可以用如图所示的两条首尾相连的线段来表示。这个含义用数学计算怎么表示呢?
我们按照数轴上的加法的思路先来看看。在数轴上,我们在做加法前,需要知道具体是哪些矢量相加,也就是这些矢量在数轴上的位置。于是,我们也在平面直角坐标系中找到这些矢量。我们来看"先往[math]\displaystyle{ x }[/math]正方向走1个单位"这句话,这就代表着一个矢量,我们记作[math]\displaystyle{ \overrightarrow{O A} }[/math],用坐标来表示为[math]\displaystyle{ (1,0) }[/math];同样,我们把"然后往y正方向走2个单位"记作[math]\displaystyle{ \overrightarrow{O B} }[/math],用坐标来表示为[math]\displaystyle{ (0,1) }[/math]。我们再来看最后停留的P点,矢量[math]\displaystyle{ \overrightarrow{O P} }[/math]用坐标可以表示为[math]\displaystyle{ (1,1) }[/math],于是你会发现,矢量[math]\displaystyle{ (1,1) }[/math]好像就是矢量[math]\displaystyle{ (0,1) }[/math]和矢量[math]\displaystyle{ (1,0) }[/math]的x坐标和y坐标分别相加。
没错,矢量的加法就是这样的规则。我们在这里总结一下[1]: 两个矢量[math]\displaystyle{ ((x_1,y_1),(x_2,y_2)) }[/math]相加的数学操作就是把两个矢量的x,y坐标值分别相加:
或者记作[1]:
例如,矢量往[math]\displaystyle{ x }[/math]正方向走1个单位([math]\displaystyle{ \overrightarrow{O A} }[/math],数学符号记为(1,0))加上矢量往[math]\displaystyle{ y }[/math]正方向走2个单位([math]\displaystyle{ \overrightarrow{O B} }[/math]或者矢量[math]\displaystyle{ \overrightarrow{A P} }[/math],数学符号记为(0,2))的计算就是:
我们得到的结果是坐标[math]\displaystyle{ (1,2) }[/math],它代表了矢量[math]\displaystyle{ \overrightarrow{O P} }[/math],也代表了点[math]\displaystyle{ P }[/math]。
矢量减法
有了矢量的加法,矢量的减法就很好定义了。与数的减法[math]\displaystyle{ a-b = a+(-1 \times b) }[/math]一样,我们把两个矢量的减法看作是一个矢量加上另一个矢量倒过来。其中倒过来也就是乘以 [math]\displaystyle{ -1 }[/math]的操作,也就是从[math]\displaystyle{ (x,y) }[/math]变成[math]\displaystyle{ (-x,-y) }[/math]。因此,矢量减法就是:
在含义上,矢量减法表示从[math]\displaystyle{ (x_2,y_2) }[/math]指向[math]\displaystyle{ (x_1,y_1) }[/math]的矢量。
矢量的旋转
(图片来源于《小学数学这样学》[1])
这里,我们再介绍一下矢量的旋转,只不过我们只介绍两种特殊的旋转,等你学会了三角函数以后,你可以总结出矢量的一般的旋转。
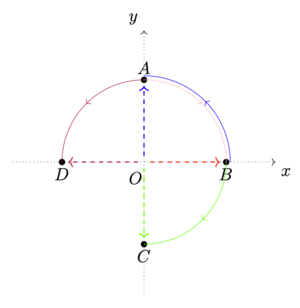
矢量的左转[math]\displaystyle{ 90^{\circ} }[/math]:你可以参照上图,想一想是怎么回事,脑子里先有矢量旋转的图形。然后你就很容易理解矢量旋转对应的坐标变换了。
比如,我们把落在x轴上的矢量[math]\displaystyle{ \overrightarrow{O B} }[/math]左转[math]\displaystyle{ 90^{\circ} }[/math],你可以在脑袋中想象一下,自然就是落在y轴正半轴上,但是由于旋转不改变矢量的长度,于是肯定还是一样长。我们假设[math]\displaystyle{ \overrightarrow{O B} }[/math]是[math]\displaystyle{ (a,0) }[/math],左转[math]\displaystyle{ 90^{\circ} }[/math]后到了y正半轴轴上,就是[math]\displaystyle{ (0,a) }[/math]。于是我们知道了,矢量左转[math]\displaystyle{ 90^{\circ} }[/math]后,x坐标和y坐标会调换,而且原来的x坐标变换为新的y坐标时,正负号也保持不变,但是要小心,至于原来的y坐标变换成现在的x坐标,正负号是什么情况,我们并不清楚,因为零既不是正数也不是负数。后面还需要进一步研究。
这时候,我们先把这个问题放一放,继续来看矢量右转[math]\displaystyle{ 90^{\circ} }[/math]:
比如,我们还是继续以[math]\displaystyle{ \overrightarrow{O B} }[/math],也就是[math]\displaystyle{ (x,0) }[/math]为例,右转[math]\displaystyle{ 90^{\circ} }[/math]后,它会落在y轴负半轴上,就是变成[math]\displaystyle{ (0,-x) }[/math]。于是我们知道了,矢量右转[math]\displaystyle{ 90^{\circ} }[/math]后,x坐标和y坐标同样也会调换,而且原来的x坐标变换为新的y坐标时,正负号要变换。但是同样要小心,至于原来的y坐标变换成现在的x坐标,正负号是什么情况,我们并不清楚,因为零既不是正数也不是负数。后面还需要进一步研究。
带着对于刚才是0的坐标变换的问题,我们来进行更进一步的研究。但是,在开始之前,由于你知道左转和右转基本上是相对应的操作,于是你需要有这样的感觉和猜想,就是矢量右转[math]\displaystyle{ 90^{\circ} }[/math]时,有[math]\displaystyle{ (x,0) \overset{右转90^{\circ}}{\rightarrow} (0,-x) }[/math];而矢量左转[math]\displaystyle{ 90^{\circ} }[/math]时,有[math]\displaystyle{ (x,0) \overset{左转90^{\circ}}{\rightarrow} (0, x) }[/math]。这对相对应的操作,对于原来的x坐标变成现在的y坐标,一个出现了正负变号,一个没有出现正负变号,而我们现在要讨论原来的y坐标到现在x坐标,我们也可以反过来对应着猜想:矢量右转[math]\displaystyle{ 90^{\circ} }[/math]时,原来的y坐标到现在的x坐标,不再出现正负号变号;矢量左转[math]\displaystyle{ 90^{\circ} }[/math]时,原来的y坐标到现在的x坐标,会出现正负号变号。(等到大学你会知道,这两个左转[math]\displaystyle{ 90^{\circ} }[/math]的操作和右转[math]\displaystyle{ 90^{\circ} }[/math]的变换,是对偶变换)
接下来我们做检验,而检验也很简单,就是对于已经左转[math]\displaystyle{ 90^{\circ} }[/math]和右转[math]\displaystyle{ 90^{\circ} }[/math]的矢量,分别再进行一次左转[math]\displaystyle{ 90^{\circ} }[/math]和右转[math]\displaystyle{ 90^{\circ} }[/math]的变换。 于是有:
所以我们的猜想得到了验证,所以我们来到最一般的矢量来总结[1]:
这里,我们顺便也简单体会了数学问题的讨论和猜想以及验证进而推广到一般情况的过程。好好体会一下,你会发现数学的魅力无处不在。
使用矢量的例题——海盗的宝藏
这部分内容摘自《小学数学这样学》[1]。
《从一到无穷大》编了一个下面这样的故事。有一个小孩得到了一张海盗藏宝图。藏宝图上记载了藏宝的海岛的地点,以及到达海岛之后怎么找到宝藏:"先找到一个海盗处理俘虏和叛徒的绞刑架,还有绞刑架旁边的两棵橡树。接着从绞刑架走到左边那棵橡树,记住走了多远,然后往右边拐一个直角走同样的步数,打下一个树桩;回到绞刑架,从绞刑架走到右边那棵橡树,记住走了多远,然后往左边拐一个直角走同样的步数,打下另一个树桩;最后,把两个树桩连起来,中间的地方就是埋下宝藏的地方。"这个小孩历经千辛万苦找到了藏宝的海岛,也差不多定位好了两棵橡树。但是,绞刑架由于年代久远只剩下一些碎木头。请你帮助这个小孩把宝藏找出来。
如果你有足够的耐心和力量,你可以把整个橡树附近的区域都挖一遍,应该可以把宝藏找出来。实际上,很多时候,我们就是通过某些信息来大概估计之后,采用穷举法,尝试了各个可能才解决问题的。不过,这发挥不了我们这一节介绍的矢量的威力,数学计算和推理的威力。今天,我们试试用矢量来解决问题。
(图片来源于《小学数学这样学》[1])
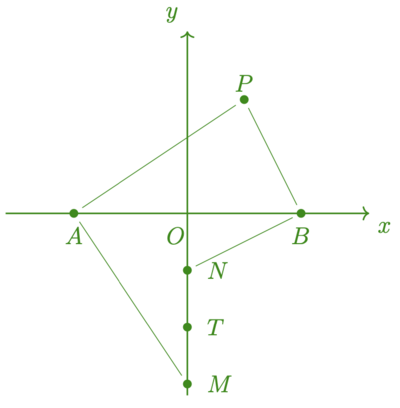
下面,我们用矢量的知识(加法、减法、旋转)、未知数的知识、带有字母的算式的计算的知识,来找找宝藏。如图所示,我们先绘制一个坐标系,原点在两棵橡树正中间(其实,原点取哪里都可以,取两棵橡树正中间仅仅是选择之一),取单位长度为原点到其中一棵橡树的距离。于是,橡树的位置分别是[math]\displaystyle{ A=(-1,0) }[/math]和[math]\displaystyle{ B=(1,0) }[/math]。然后,我们假设那个绞刑架在一个坐标为[math]\displaystyle{ P=(x,y) }[/math]的地方(注意P肯定在两棵橡树之间的某个地方)。我们来照着海盗的留言做:"从绞刑架走到左边那棵橡树"A的地方,记下来走了多远,也就是
然后"右拐"也就是右转,得到[math]\displaystyle{ \overrightarrow{P A}=(y, -x-1) }[/math],于是M点的坐标是:
接着回到绞刑架,往右边的橡树走接着左拐得到另一个点N,
最后,我们取两个点的中间的点,也就是把M,N两个点的坐标加起来除以二,得到:
这也就是原点下方y轴反方向1个单位长度的地方,也就是在绞刑架的另一侧找到在AB的中垂线上,从AB的中点开始距离为AB距离的一半的点。
更进一步,如果绞刑架一点影子都没有了,也没关系,那就把两棵橡树之间的y轴正方向和反方向距离原点为两棵橡树之间距离一半的地方都挖开看看。这也要比在橡树附近挖很多很多个坑效率高多了。数学,就是通过思考来更高效地解决问题的方法。数学就是思维的语言,通过计算可以更好地做深入的思考。
本分类目前不含有任何页面或媒体文件。