定义和含义

圆周率，通常用希腊字母[math]\displaystyle{ \pi }[/math]表示，是数学中的一个基本常数，定义为一个圆的周长与其直径的比。圆周率是一个无理数，是一个无限不循环小数。通常，我们在计算时，常用[math]\displaystyle{ 3.14 }[/math]来做计算。

层次标注

在这里，它属于第二层知识，即学科概念。

从圆的周长得到圆周率

由于周长的单位是长度单位，而圆的半径的单位也是长度单位，所以圆的周长理论上来说，就是一个未知的常数乘上半径，可以写为：[math]\displaystyle{ C = 常数\Pi \times R }[/math]，这里[math]\displaystyle{ R }[/math]是半径。

目前，我可以直接告诉你，这个常数[math]\displaystyle{ \Pi }[/math]是圆周率的2倍，大约等于6.28。

但是，这个数是怎么来的呢？

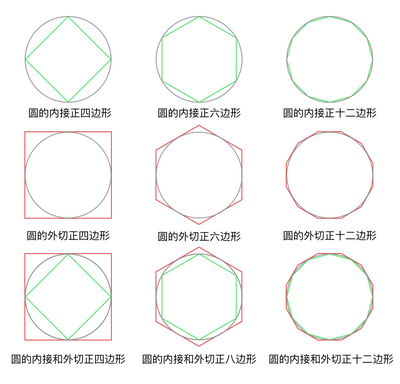
我们来看两个和圆相关的概念，圆的内接多边形和圆的外切多边形。

圆的内接正多边形，指的是，一个正多边形的所有顶点正好都在圆上，这样的正多边形我们称为圆的内接正多边形。

圆的外接正多边形，指的是，一个正多边形的所有边都正好和圆相切。这里所谓的相切，就是多边形的一条边和圆正好只有一个交点。这样的正多边形我们称为圆的外切正多边形。

圆的内接和外切正多边形

我们可以从图中直观的看到，对于同一个圆来说(我们假设这四个圆是一样大的)，随着正多边形的边数增加，外切正多边形的周长在逐渐缩小以靠近圆的周长，与此同时，内接正多边形的周长在逐渐增加以靠近圆的周长。这时候，如果我们继续思考，如果这两个正多边形的周长不断增加，那么中间留给圆的周长的部分也就越来越小，似乎就是用两个正多边形的周长就可以把圆的周长夹在中间挤压，最后这两个正多边形的周长都会非常靠近圆的周长，这样就可以把圆的周长大致确定下来了。

也就是说，

这里，我们有4组数据，是已经算好了的。(至于怎么算，如果你学了三角函数后，你可以借助计算器来算任意边数的正多边形的周长。在这里，如果你会勾股定理，那么你可以算一下当内接和外切的都是正四边形时的情况。另外，你可以用外切正六边形和内接正六边形算一下看看，因为正六边形是特殊的正多边形，如果你把圆心和各个顶点连起来后，你会发现正三角形，而正三角形是三边全等的三角形，而这里面的斜边和邻边以及对边的比值，你可以通过查表得到，如果没有表，也可以去使用计算器来帮助你。)

当内接和外切的都是正四边形时：[math]\displaystyle{ 5.656r \lt 圆的周长 \lt 8r }[/math] ，也就是 [math]\displaystyle{ 5.656 \lt \Pi \lt 8 }[/math]

当内接和外切的都是正六边形时：[math]\displaystyle{ 6 \lt \Pi \lt 6.928 }[/math]

当内接和外切的都是正十二边形时：[math]\displaystyle{ 6.212 \lt \Pi \lt 6.431 }[/math]

当内接和外切的都是正二十四边形时：[math]\displaystyle{ 6.265 \lt \Pi \lt 6.319 }[/math]

这时候，你是不是就能看到圆的周长随着内接和外切的正多边形的边数增加，范围越来越小，似乎是越来越可以有一个差不多能够用来估计的值了。还记得在上面，我告诉过你，圆的周长大约是半径的6.28倍吗？

这里，这样两头向中间挤压的来估计一个未知数的值的思维方式，叫作夹逼的思想。另外，通过不断去增加参数的值，最后甚至是用脑袋去思考如果一直增加下去的会怎么样的思维方式，叫作极限的思想。

以后试着再其他问题上体会一下这两个思想。

为了统一符号，我们记这个常数[math]\displaystyle{ \Pi }[/math]为[math]\displaystyle{ 2\pi }[/math]，并且在计算中用[math]\displaystyle{ \pi \approx 3.14 }[/math]，于是我们有圆的周长和半径的关系是^[1]：

而这里的[math]\displaystyle{ \pi }[/math]，就是圆周率。