分类:命题
定义和含义
命题,指的是,一句带有潜在的集合关系的话,这句话本身是一句陈述句,我们就称之为一个命题。最常见的就是"什么什么是什么"、"什么什么有什么"、"什么什么具有什么性质"的话[1]。一般来说,我们都可以判断命题的真假,如果命题陈述的内容是真的,那么这个命题就为真;反之,如果命题陈述的内容是假的,那么这个命题就为假。
在演绎推理中,一般的,我们把命题看作是一个条件 [math]\displaystyle{ A }[/math] 和一个结论 [math]\displaystyle{ B }[/math] 的结合, 表示在这个条件 [math]\displaystyle{ A }[/math] 下 [math]\displaystyle{ B }[/math] 这个结论肯定正确,记作 [math]\displaystyle{ A \Rightarrow B }[/math][1] 。
对于这些命题,我们最关心的是它们背后的集合关系。
这样的命题都可以表述成如下的形式: [math]\displaystyle{ A }[/math] 具有性质 [math]\displaystyle{ B }[/math] , 记作 [math]\displaystyle{ A \Rightarrow B }[/math] (读作 [math]\displaystyle{ A }[/math] 推出 [math]\displaystyle{ B }[/math] 、 [math]\displaystyle{ A }[/math] 导出 [math]\displaystyle{ B }[/math] 、 [math]\displaystyle{ A }[/math] 具有 [math]\displaystyle{ B }[/math] 等),表示如果一个东西具有性质 [math]\displaystyle{ A }[/math] 则这个东西肯定具有性质 [math]\displaystyle{ B }[/math]。
有了集合的语言和集合之间的关系,我们来用集合直观地展示命题和否命题、逆命题和逆否命题的关系[1]。这些关系是逻辑的底层关系。所以一定程度上可以说,逻辑的背后其实是集合。
层次标注
在这里,它属于第二层知识,即学科概念。
辅助理解的解释
例如,"等式具有两边同时加上一个数等号不变的性质" 的 [math]\displaystyle{ A }[/math] 是 "如果一个东西是等式", [math]\displaystyle{ B }[/math] 是 "两边同时加上一个数仍然是等式",或者也可以看作 [math]\displaystyle{ A }[/math] 为 "如果对一个等式的两边加上同一个数", [math]\displaystyle{ B }[/math] 就是 "等号不变"。
逻辑命题的三定律
一般来说,命题需要符合这三条定律:
同一律,指的是,一个命题不能表达着两个意思,命题中表达的意思是清清楚楚的。
无矛盾律,指的是,一个命题不能同时既为真又为假。
排中律,指的是,一个命题不是真的就是假的。
对于上面的内容,我们来稍微总结一下,一个命题必须要说的清清楚楚,而且可以判断真假。
有了这些性质,我们才能说,反证法是严格意义上的演绎推理。当然,我们后面还会看到从集合的角度来看反证法的逻辑严密性。
其实,在你有了集合的概念以后,你会发现,这些性质都是来源于集合中的元素的明确性的性质的拓展,由于集合中的元素必须是明确的,你可以清楚的知道一个元素是归属于哪个集合的,于是在命题的范畴上衍生出了了命题这三点性质。于是,当你明白了元素和集合的概念,而且有了深刻的集合的思想,命题的性质你是自然就会明白的,不用去记住。
命题和集合的联系
这部分内容摘自《小学数学这样学》[1]:
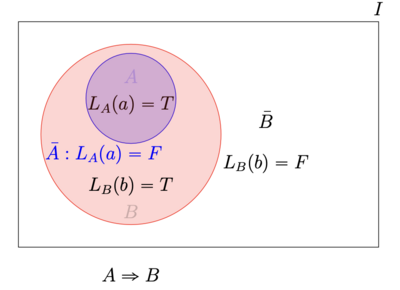
在这里, 为了建立这个从集合到命题的联系,我们先把 [math]\displaystyle{ A \Rightarrow B }[/math] 的 [math]\displaystyle{ A }[/math] 和 [math]\displaystyle{ B }[/math] 分别看作集合:集合 [math]\displaystyle{ A^{1} }[/math] 就是 那些具有性质 [math]\displaystyle{ A }[/math] 的事物的集合。例如,在 "三角形的内角是 [math]\displaystyle{ 180^{\circ} }[/math] " 中就是 "所有的三角形"。类似地,集合 [math]\displaystyle{ B }[/math] 就是具有性质 [math]\displaystyle{ B }[/math] 的事物的集合。例如在 "三角形的内角和是 [math]\displaystyle{ 180^{\circ} }[/math] " 中就是 "内角和是 [math]\displaystyle{ 180^{\circ} }[/math] 的封闭图形"。于是,我 们发现,如果一个命题 [math]\displaystyle{ A \Rightarrow B }[/math] 成立,用集合的语言就是集合 [math]\displaystyle{ A }[/math] 包含在集合 [math]\displaystyle{ B }[/math] 之中,如图所示。
(图片来源于《小学数学这样学》[1])
集合 [math]\displaystyle{ A }[/math] 中的元素 [math]\displaystyle{ a }[/math] 是通过 [math]\displaystyle{ L_{A}(a)=T }[/math] 来定义的, 也就是所有具有性质 [math]\displaystyle{ A }[/math] 的元素。集合 [math]\displaystyle{ B }[/math] 中的元素 [math]\displaystyle{ b }[/math] 是通过 [math]\displaystyle{ L_{B}(b)=T }[/math] 来定义的, 也就是所有具有性质 [math]\displaystyle{ B }[/math] 的元素。(这里的T就是TRUE的缩写,意思就是命题为真;F就是FULSE的缩写,意思是命题为假)
于是, 只要 [math]\displaystyle{ A \subset B }[/math] , 则具有性质 [math]\displaystyle{ A }[/math] 的元素 [math]\displaystyle{ a\left(L_{A}(a)=T\right) }[/math] 必然具有性质 [math]\displaystyle{ B\left(L_{B}(a)=T\right) }[/math] ,也就是 [math]\displaystyle{ A \Rightarrow B }[/math] 。把命题和集合之间得关系联系起来对于数学论证是非常重要的。