定义和含义

代数的思想^[1]，就是使用代数去思考和解决问题的思维方式和分析方法，这种思维方式突破了具体对象的局限性，强调一般性和抽象性，从而使得问题中的对象之间的关系的描述和求解更为系统化和普遍化。

层次标注

在这里，它属于第三层知识，即学科大图景。

辅助理解的解释

在数的学习中，我们体会到了从算筹到数字的抽象过程，这样的抽象使得我们可以用初步用数学的语言来思考问题，来描述世界。而现在，我们要更进一步，我们不再满足于从算筹到数字的抽象，我们要脱离具体的数字，走向字母，用字母替代具体的数字，用于表达一切适用于当前数学关系的对象。

在这里，有了代数以后，我们对于数学的研究就不再限制于对象了，转而关注对象之间的关系。

代数的思想根源还是来自于抽象，帮助我们认清事物之间的规律和联系^[2]。

比如说，加法就是把两个数a和b加起来，写作 [math]\displaystyle{ a + b }[/math] ，在知道了代数以后，以后可以用字母来代表一个一般的数，它可以用任何一个具体的数来代入^[1]。

同样的，请你试着思考和写下用代数表示的减法、乘法和除法。

一定程度上来说，它其实是抽象的更具体的表述，是一种使用抽象的对象来替代具体的对象的更一般的思考问题的方式，帮助我们在抽象层面进行思考，从而在思考上走的更深刻走的更远。

一个例子来体会代数的思想的威力

下面这个例子摘自《小学数学这样学》^[1]：

桌子上的猫(代数的思想的例子)

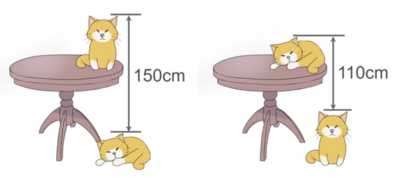
有两只完全一样的猫，还有一张桌子。左边是一只在地上趴着，一只在桌子上站着。右边是一只在地上站着，一只在桌子上趴着。我也不知道为什么，有人测量出来了两只猫之间的高度差。请你来算算桌子的高度。

我们用字母 [math]\displaystyle{ T }[/math] 表示桌子的高度, [math]\displaystyle{ C_s }[/math] 表示站着的猫的高度, [math]\displaystyle{ C_l }[/math] 表示趴着的猫的高度。注意，这里我们就用了字母来表示数，表示事物的量。我们再来看这些高度和测量出来的高度差之间的关系。

我们发现，左边和右边分别是 :

现在，我们把两个算式相加(请思考为什么可以把两个等式加起来)，得到:

因此 [math]\displaystyle{ T=130(厘米) }[/math]

我们发现，一旦我们去观察两个等式，注意到这两个等式之间的关系 —— [math]\displaystyle{ T+C_s-C_l }[/math] 和 [math]\displaystyle{ T+C_l-C_s }[/math] 的联系，就很容易发现，只要我们把两个等式相加，就可以去掉那些不知道是多少的 [math]\displaystyle{ C_s }[/math] , [math]\displaystyle{ C_l }[/math] 。这样的一个观察，如果我们没有代数的思想——用字母来代表数和算式，是完全不可能得到的。