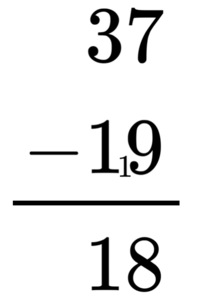定义和含义

借位，指的是，在进行算术运算时，当某一数位上的数字不够进行运算时，就需要从更高一位的数位上“借”来一部分，把这部分和原来的部分合起来进行运算，来帮助完成运算的过程。

层次标注

在这里，它属于第一层知识，即程序性知识。

辅助理解的解释

减法借位的竖式例子

例如，在进行减法时，当某一数位上的数字小于被减数时，也就是数字已经不够减了，就需要从更高一位的数位上“借”来一个1帮助完成减法运算的过程。在十进制系统中，这意味着从更高的数位借来了10，因为更高一位的1其实相当于低一位的10。(这里，等你彻底学会了进制系统，你会明白为什么)

无论在什么进制系统中，数位上的数字最小只能是0，如果遇到0还需要再减去任何数字的情况，就需要借位。

例如， [math]\displaystyle{ 23 - 4 = 19 }[/math] ，这里被减数23中的2是在十位上的数字，3是在个位上的数字；而减数4是在个位数上的数字。这时候两个数相减时，个位数上的减法是3-4，已经出现了不够减的情况，于是需要向更高位来借位，于是就有[math]\displaystyle{ 13-4=9 }[/math]，此时结果的个位数上的数是9，而被减数的十位数上的数由于被借位借走了1，所以只剩下了1，所以最后的结果是19 。

下面，我们来看一个列竖式计算的减法的例子，其中就包含了借位的过程。你在刚开始接触借位时，就可以利用列竖式计算来帮助你完成准确的涉及借位的减法计算。

竖式中间的那个小小的1，就是表示个位数相减以后，需要向更高位，也就是十位，借来1 。于是，我们在计算十位上的[math]\displaystyle{ 3-1 }[/math]时，还需要额外把写下来的借位得来的小小的1也减去，变成了[math]\displaystyle{ 3-1-1 }[/math]，于是等于1 。所以我们得到了结果18。