定义和含义

两条直线平行同位角相等定理，指的是，三条直线相交，两条直线平行，则同位角相等^[1]。

层次标注

在这里，它属于第二层知识，即学科概念。

对这个定理进行数学证明

这个定理的证明基于平行线判定定理，使用反证法进行。

以下是摘自《小学数学这样学》的证明内容^[1]：

平行线性质定理

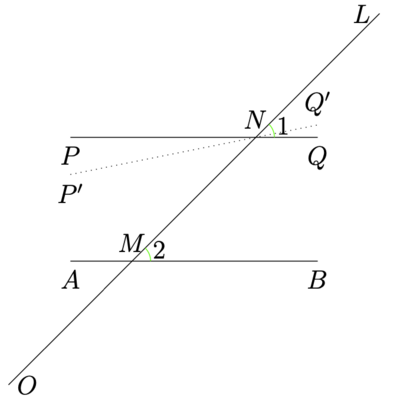
(图片来源于《小学数学这样学》^[1])

证明：我们假设同位角不相等, 例如图中所示的上方的 [math]\displaystyle{ \angle 1 }[/math] 大于下方的 [math]\displaystyle{ \angle 2 }[/math] 。我们用尺规作图在 [math]\displaystyle{ \angle 1 }[/math] 内部作一个和 [math]\displaystyle{ \angle 2 }[/math] 相同的角, 以 [math]\displaystyle{ N }[/math] 为顶点, 以 [math]\displaystyle{ N L }[/math] 为固定边, 得到 [math]\displaystyle{ P^{\prime} Q^{\prime} }[/math] 。

按照平行线判定定理 (注意平行线判定定理不依赖于三角形内角和公理, 所以这里可以使用), [math]\displaystyle{ P^{\prime} Q^{\prime} \| A B }[/math] 。已知, [math]\displaystyle{ P Q \| A B }[/math] , 且两条直线都过 [math]\displaystyle{ N }[/math] 点, 因此得到过直线外一点有两条直线和给定的直线平行。这个和平行线唯一性公理矛盾。

因此，原假设错误，也就是同位角相等。