定义和含义

极限的思想是，在一种运算或数学结构中，如果重复一直做下去，一直到无穷，就会越来越靠近某一种比较稳定的结果或者情况，这样的思想被称为极限的思想。

辅助理解的解释

圆内接和外切多边形

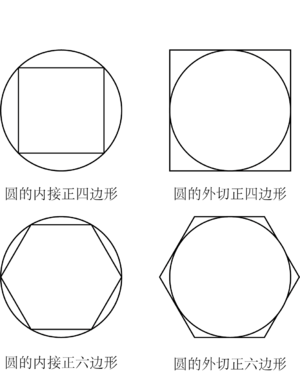
在没有圆周率 [math]\displaystyle{ \pi }[/math] 的前提条件下，如果需要解算圆的周长，可以考虑使用圆的内接多边形或者是圆的外切多边形的方法来近似的计算。

这个方法利用了极限的思想，通过逐渐增加多边形的边数来逼近圆的周长。可以通过从内接（外切）四边形，到内接（外切）六边形，直观的感受到多边形的周长在不断靠近圆的周长。

而且对于正多边形，我们很容易能计算出它的周长。因此，随着边数不断增加，甚至增加成"无穷多边形"，那么我们就可以说这个"无穷多边形"的周长就是圆的周长。这里的“无穷”，就是极限的思想的直接体现。

虽然这不是一个精确的计算方法，但当边数足够大时，我们可以得到非常接近实际圆周长的结果。

鼓励你去多思考和体会还有哪些地方可以使用极限的思想来解决问题。

另外，在你计算圆的同一个内接和外切的多边形时，有没有发现圆的周长和这两个多边形的周长有什么关系？（这里值得思考，体现的是夹逼的思想）