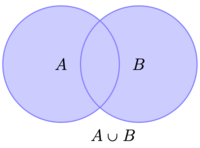
分类:并集
来自Big Physics
定义和含义
并集,指的是,在集合 [math]\displaystyle{ A }[/math] 里面或者在集合 [math]\displaystyle{ B }[/math] 里面的东西合起来的集合,称作 [math]\displaystyle{ A, B }[/math] 的并集[1],记作"[math]\displaystyle{ A \cup B }[/math]",表示集合 [math]\displaystyle{ A }[/math] 和集合 [math]\displaystyle{ B }[/math] 的并集。
(图片来源于《小学数学这样学》[1])
层次标注
在这里,它属于第二层知识,即学科概念。
辅助理解的解释
例如, 如果 [math]\displaystyle{ A=\{1,2,3\} }[/math] 和 [math]\displaystyle{ B=\{3,4,5\} }[/math] , 那么 [math]\displaystyle{ A \cup B= \{1,2,3,4,5\} }[/math] 。
通俗来说,并集可以被看作是将两个或多个集合的元素放在一起,形成一个新的集合。
在计算并集时,要注意并集的结果还是一个集合,一个集合也就需要去关注集合本身的定义,也就是集合中的元素要具备确定性、互异性和无序性。其中,最应该关注的互异性,也就是并集以后,仍然不能有重复的元素。
- ↑ 1.0 1.1 吴金闪,《小数数学这样学》,浙江人民出版社,2023, http://www.systemsci.org/jinshanw/books
本分类目前不含有任何页面或媒体文件。