分类:分数

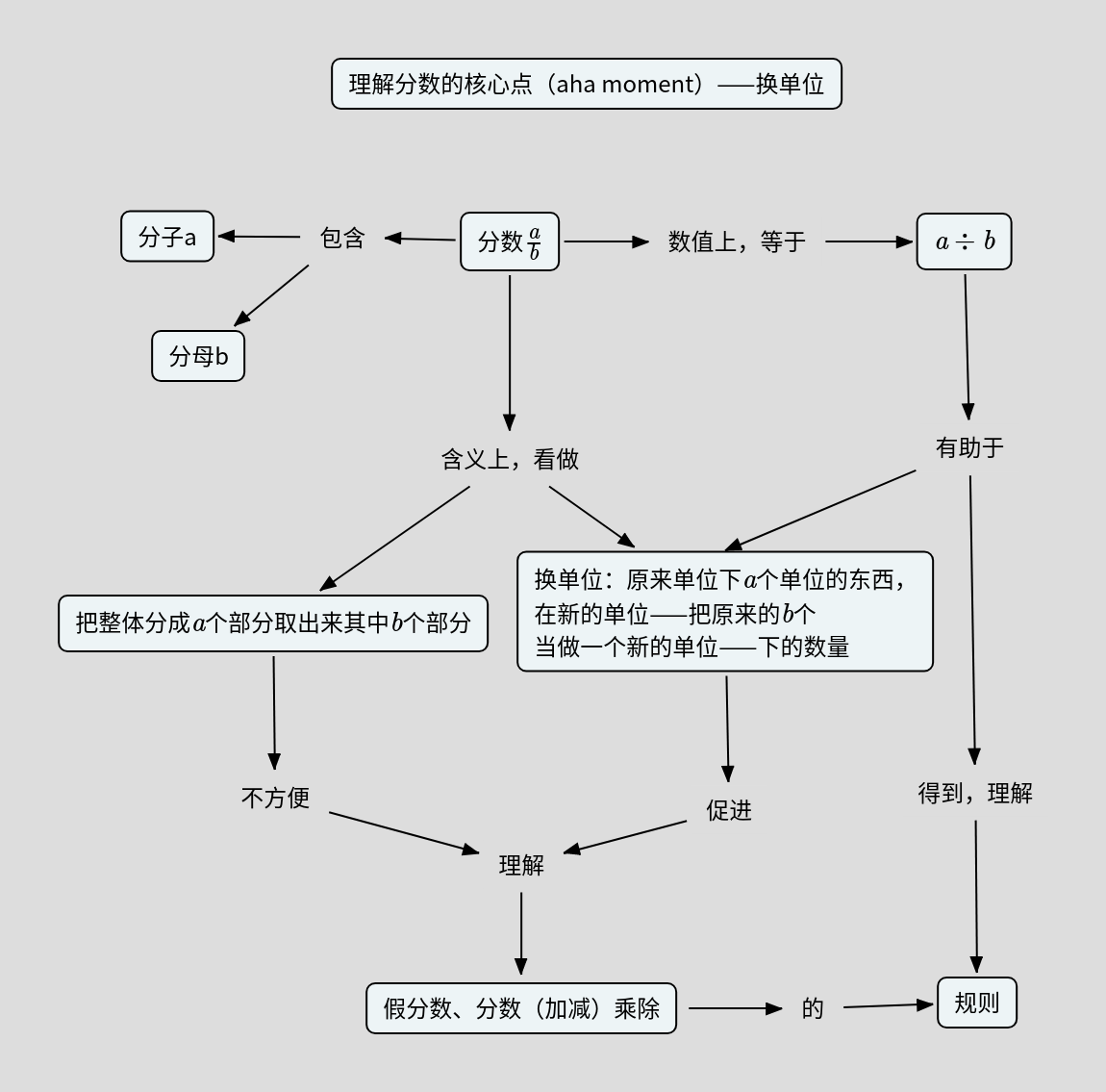
分数是一个比较抽象的概念。

分数的直观理解是“把一个整体分成若干（分母的数量）份，从中取出来若干（分子的数量）份”。但是，这个理解将来遇到假分数、分数乘法、分数除法的时候都会出问题。

分数的另一个理解是“两个数相除（分子除以分母）得到的结果”。这个理解是基本上把分数当做小数来理解，对是很对，但是，通过计算来定义数这个比较抽象。当学习者的抽象思维能力还不够的时候，这个理解也很难用来帮助学习者更好地理解分数的加减乘除。

那么，有没有一个分数的理解方式，既不是那么抽象，有完全能够起到帮助学习者将来更好地理解分数的加减乘除呢？有，把分数看作是“一个东西的量在改变单位之后的数值”。例如，[math]\displaystyle{ \frac{1}{5} }[/math]就是把原来的单位度量下的[math]\displaystyle{ 5 }[/math]个看做新的一个单位的时候的数量。在这个理解下，分数和整数的乘法，自然就可以直接把分子乘起来，然后再换单位；分数和分数的加法，自然要先带着单位，然后统一单位，最后来相同的单位下来相加。

更一般地，我们认为，所有的数的概念、数学计算的教和学，甚至应用和理解，都应该从带这单位的带着具体情境的形式开始，然后一般化到不依赖单位的纯数的形式。