决策和博弈理论的基本框架

一般来说，经典博弈论和经典决策理论假设经典概率论成立。经典概率论指的是，一个随机事件的多种可能的出现概率由概率分布函数（以离散变量为例）[math]\displaystyle{ \rho=\sum_{i}P_{i}\left|i\right\rangle\left\langle i\right| }[/math]描述，给定一个观测量[math]\displaystyle{ X=x_{i}\left|i\right\rangle\left\langle i\right| }[/math]，则这个观测每次会得到一个[math]\displaystyle{ x_{i} }[/math]以及相应的随机事件的状态[math]\displaystyle{ i }[/math]，如果重复多次测量则当次数[math]\displaystyle{ M }[/math]足够大的时候，[math]\displaystyle{ M\rightarrow \infty }[/math]，其均值满足[math]\displaystyle{ \left\langle X\right\rangle \triangleq \frac{\sum_{i}x_{i}}{M} \rightarrow tr\left(\rho X\right)=\sum_{i}x_{i}P_{i} }[/math]。

在这个假设的基础上，决策问题可以看作是约束下的极值问题，博弈问题可以看作是在给定对方策略下的决策问题，其中对方策略本身按照完全理性的假设，是给定自己的决策下的对方的决策问题的解。通常我们会有一个目标函数，称为收益函数，例如决策问题的[math]\displaystyle{ X=\sum_{i}x_{i}\left|i\right\rangle\left\langle i\right| }[/math]，或者博弈问题的[math]\displaystyle{ X=\sum_{ij}x_{ij}\left|ij\right\rangle\left\langle ij\right| }[/math]。按照经典概率论，则当一个决策者，或者一对决策者，采取策略[math]\displaystyle{ \rho^{1}=\sum_{i}P^{1}_{i}\left|i\right\rangle\left\langle i\right| }[/math]，[math]\displaystyle{ \rho^{12}=\sum_{ij}P^{12}_{ij}\left|ij\right\rangle\left\langle ij\right|=\sum_{ij}P^{1}_{i}P^{2}_{j}\left|ij\right\rangle\left\langle ij\right| }[/math]的时候，其收益（对于完全理性人的决策和博弈理论，这个收益也被称为效用）为[math]\displaystyle{ u = tr\left(\rho X\right)=\sum_{i}x_{i}P_{i} }[/math]，以及[math]\displaystyle{ u = tr\left(\rho^{12} X\right)=\sum_{ij}x_{ij}P^{1}_{i}P^{2}_{j} }[/math]。

于是，传统的决策和博弈理论就成了如何根据这个效用函数[math]\displaystyle{ u }[/math]以及相应的约束（没有写出来）来优化，求出来最优解，然后用这个最优解对应的策略当做对决策者行为的描述。或者更一般地，给出来一个每个策略[math]\displaystyle{ i }[/math]被选择的几率[math]\displaystyle{ Q_i }[/math]。为了以后描述问题方便，我们把有了效用函数之后，再通过求极值来解决问题的思路称为“效用函数最大化”。

一个理论框架的成立，需要通过实验来检验，是否在适当的现象的范围内，理论给出的结果和实验结果在误差范围相符。

研究问题

实际上，上面这个漂亮的决策和博弈的理论框架，很多时候不符合实验结果和实际观察。例如，在概率匹配现象中，决策者的决策显然和最优策略不同，见概率匹配的决策机制；在囚徒困境、最后通牒博弈中，实验者的行为也显然后上面的理论预测的博弈者行为有很大差别，见概率测试和最后通牒研究；博弈实验的结果已经展示了对上面这个“完全概率和条件概率的关系”的突破，见突破概率叠加的经典实验结果。研究者把这些理论和实验实践的偏离统一称为“非完全理性人”的决策。

因此，我们的研究问题是：是否能够构建一个非完全理性人的描述框架来描述上面这些行为。更进一步，如果说，我们仅仅需要改变效用函数的具体形式，仍然维持“效用函数最大化”，那这个理论跟传统决策和对策理论相比所做的修改就比较少。我们当然还可以突破“效用函数最大化”，那如果发现不突破的话理论模型就是描述不了实验，那就突破。但是，我们尽量先做最少量的修改。

解决方法：构建新的理论框架

下面，我们来尝试以下两种可能的模型。

修改效用函数，但是保持效用函数最大化

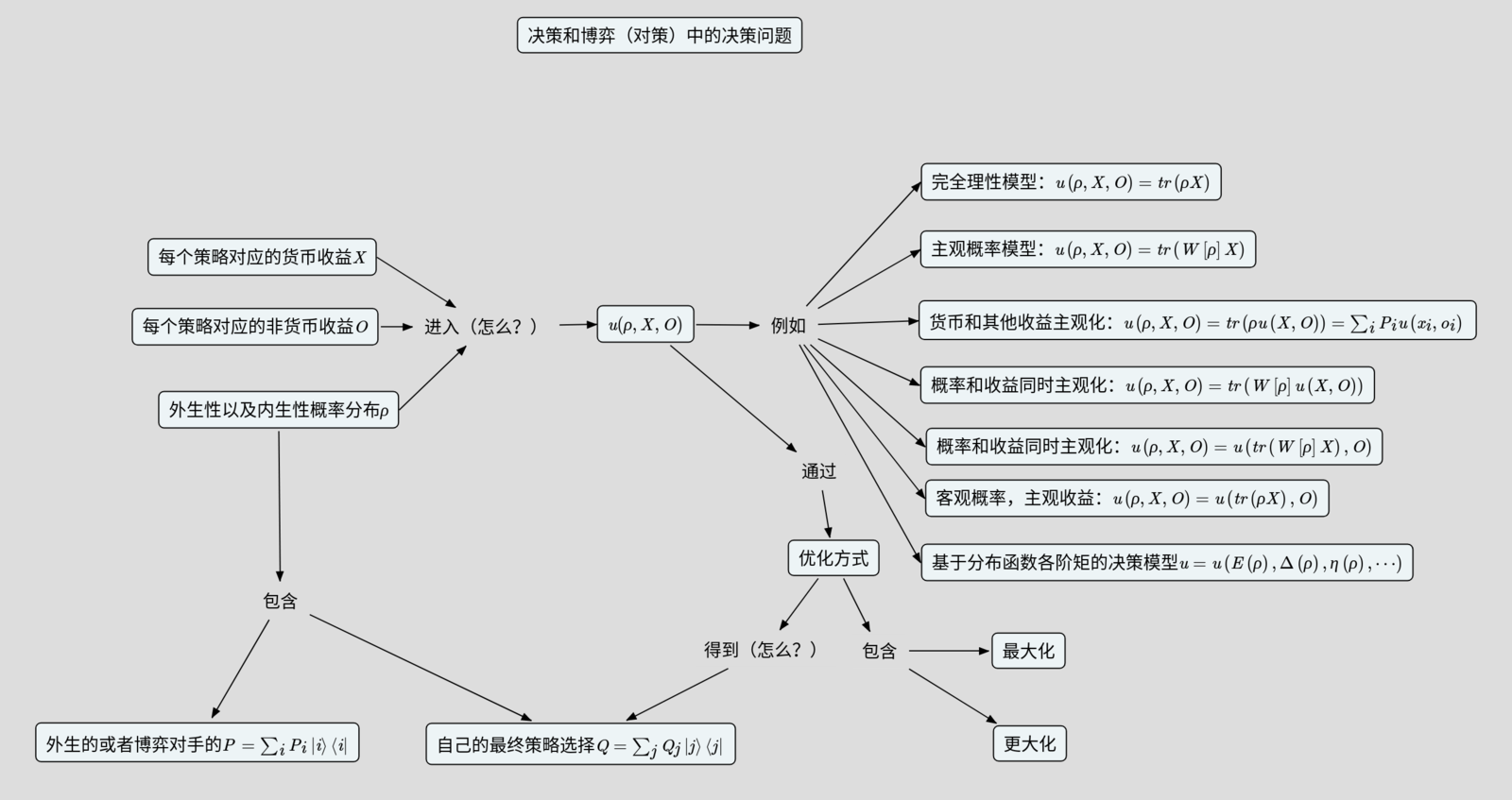
在这里，我们通过引入货币收益之外的因素、对收益的主观感受、对概率的主观感受，来构建新的决策和博弈的理论框架，例如下面的一个完全理性个体的标准模型以及五个非完全理性人决策的模型：

1. 经典完全理性个体的决策理论，客观概率－客观货币收益：[math]\displaystyle{ u=\sum_{i}P_{i}x_{i} }[/math]
2. 主观概率－客观货币收益：[math]\displaystyle{ u=\sum_{i} W\left[P_{i}\right]x_{i} }[/math]
3. 客观概率－主观收益：[math]\displaystyle{ u=\sum_{i} P_{i}u\left(x_{i},o\right) }[/math]
4. 主观概率－主观收益：[math]\displaystyle{ u=\sum_{i} W\left[P_{i}\right]u\left(x_{i},o\right) }[/math]
5. 客观概率平均收益的主观衡量：[math]\displaystyle{ u=u\left(\sum_{i}P_{i}x_{i},o\right) }[/math]
6. 主观概率平均收益的主观衡量：[math]\displaystyle{ u=u\left(\sum_{i}W\left[P_{i}\right]x_{i},o\right) }[/math]

当[math]\displaystyle{ W\left[P_{i}\right]=aP_{i}+b, u\left(x_{i},o\right)=u\left(x_{i}\right)=fx_{i}+g }[/math]都是线性函数的时候，所有的模型回到完全理性个体的标准模型。

于是，现在的研究问题就成了，能不能写下来适用于决策和博弈实验以及现象的[math]\displaystyle{ W\left[P_{i}\right], u\left(x_{i},o\right) }[/math]，包含哪些[math]\displaystyle{ o }[/math]？

抛弃最大化，改成效用函数更大化

也就是说，决策的时候，我们不是寻找最优的，而是只能做到“更优的策略被选择的可能性更高”——这个我们叫做“更大化”的策略。例如，采用Boltzmann分布的形式，[math]\displaystyle{ Q_{i}=\frac{e^{\beta u\left(x_{i},o\right)}}{\sum_{j} e^{\beta u\left(x_{j},o\right)}} }[/math]（注意这里这个决策者选择[math]\displaystyle{ i }[/math]的几率和给定的[math]\displaystyle{ i }[/math]出现的几率[math]\displaystyle{ P_i }[/math]不是一个东西）。其实，经济学家也已经提出了这个框架，例如博弈理论中的QRE（Quantal Response Equilibrium，随机反应均衡）^[1][2]。当然，可能还有其他的代替最优化的理论框架。

于是，研究问题就成了，如果我们允许主观概率和主观收益，以及非货币收益，并且允许用“更大化”代替“最大化”，是否我们就可以得到描述决策和博弈行为的实验结果的理论？如果可以，这些函数的具体形式，包含哪些变量，以及“更大化”的具体形式，都长什么样？

新的框架：基于分布函数各阶矩的决策模型

换一个角度，我们把效用函数看作是分布函数各阶矩的函数，例如[math]\displaystyle{ u=u\left(E\left(\rho\right), \Delta\left(\rho\right), \eta\left(\rho\right), \cdots\right) }[/math]，其中[math]\displaystyle{ E\left(\rho\right), \Delta\left(\rho\right), \eta\left(\rho\right) }[/math]分别是[math]\displaystyle{ \rho }[/math]以及对应着的货币收益、非货币收益整合在一起的各阶矩。例如[math]\displaystyle{ E\left(\rho\right)=\sum_{i}P_{i}u\left(x_{i},o_{i}\right) }[/math]。

于是，研究问题就成了，如果构建一个用分布函数各阶矩当做自变量的决策模型，然后用“最大化”或者“更大化”，是否可以描述决策行为。如果可以，这个函数的具体形式是什么，包含哪些变量？

当然，我们顺便还得回答：是不是任何前面的模型，都存在一个对应的各阶矩的表达。如果是，我们就有了决策和博弈理论框架的另一种表示。

下面，我们将从各个具体博弈的研究来回答上面两方面的问题。

传统理论及其和新框架的关系

我们在风险态度的测量已经做了总结。现在重新整理在这里。

首先，当然是完全理性决策模型，假设决策者仅仅考虑货币收益、决策者对概率的认知完全客观、决策者采用效用函数的最大值对应的决策。这也就是决策者通过求解[math]\displaystyle{ u=\sum_{i}Q_{i}P_{i}x_{i} }[/math]的最大值对应的[math]\displaystyle{ Q_{i} }[/math]做决策。于是，决策者自然会选择[math]\displaystyle{ P_{i}x_{i} }[/math]最大的那个[math]\displaystyle{ i }[/math]。这就是期望收益理论——人们选择期望收益最大的策略或者行动。推而广之，如果一个策略本身有多个可能的结果，则按照这个策略的平均收益[math]\displaystyle{ u_{i}=\sum_{j}P^{j}_{i}x^{j}_{i} }[/math]来决策。

其次，期望效用理论，[math]\displaystyle{ u=\sum_{i}Q_{i}P_{i}u\left(x_{i},o_{i}\right) }[/math]，也就是对收益部分引入非线性。

接着，前景理论（主观概率期望收益），[math]\displaystyle{ u=\sum_{i}Q_{i}W\left[P_{i}\right]x_{i} }[/math]，也就是对外生概率引入非线性。

这些都是前人已经提出的理论（天笑，加上参考文献）。

然后，我们还可以尝试拓展的前景理论（主观概率期望效用），[math]\displaystyle{ u=\sum_{i}Q_{i}W\left[P_{i}\right]u\left(x_{i},o_{i}\right) }[/math]，对外生概率和收益同时引入非线性。以及另外两种同时引入这两个非线性的理论，客观概率平均收益的主观衡量：[math]\displaystyle{ u=u\left(\sum_{i}Q_{i}P_{i}x_{i},o\right) }[/math]，主观概率平均收益的主观衡量：[math]\displaystyle{ u=u\left(\sum_{i}Q_{i}W\left[P_{i}\right]x_{i},o\right) }[/math]。

最后，其实，我们可以对外生概率和自己的概率同时引入非线性：[math]\displaystyle{ u=\sum_{i}W\left[Q_{i}\right]W\left[P_{i}\right]u\left(x_{i},o_{i}\right) }[/math]，以及相应的另外两种可能。当然，对自己的概率引入非线性是什么意思，我还不知道。大概就是，“我”主观上会不一定把[math]\displaystyle{ \frac{1}{10} }[/math]的外生概率看做真的是[math]\displaystyle{ \frac{1}{10} }[/math]：例如当这个概率是获得或者失去一笔钱的时候，我会缩小或者放大这个概率；同时，对于我即将以[math]\displaystyle{ \frac{1}{10} }[/math]的概率去做某件事情的时候，依赖于这件事情的结果是获得还是失去，也会导致不同的主观概率感受。那么，会存在这样的现象吗，是不是引入这个非线性之后就可以解释更多的现象呢？

参考文献