定义和含义

原定理（[math]\displaystyle{ P=1\Rightarrow Q=1 }[/math]，或者记做[math]\displaystyle{ P\Rightarrow Q }[/math]，读作“条件[math]\displaystyle{ P }[/math]成立的时候则条件[math]\displaystyle{ Q }[/math]必然成立”）和逆否定理（[math]\displaystyle{ Q=0\Rightarrow P=0 }[/math]，或者记做[math]\displaystyle{ \bar{Q}=1\Rightarrow \bar{P}=1 }[/math]或者更简单地[math]\displaystyle{ \bar{Q}\Rightarrow \bar{P} }[/math]，读作“条件[math]\displaystyle{ Q }[/math]不成立的时候则条件[math]\displaystyle{ P }[/math]也必然不成立”）等价，在数学中是一个非常重要的结论。通常在数学的教和学中，这个结论是当做一个毋庸置疑的类似公理的东西的，但是，实际上，这个是一个定理，完全可以用集合论的语言来证明的。

顺便，如果[math]\displaystyle{ P=1\Rightarrow Q=1 }[/math]，我们称[math]\displaystyle{ P }[/math]是[math]\displaystyle{ Q }[/math]的充分条件，并且，正是由于有了原定理和逆否定理的等价性，我们才能说，[math]\displaystyle{ Q }[/math]是[math]\displaystyle{ P }[/math]的必要条件，也就是说如果[math]\displaystyle{ Q }[/math]不成立，[math]\displaystyle{ \bar{Q}=1 }[/math]（[math]\displaystyle{ Q=0 }[/math]）则[math]\displaystyle{ \bar{P}=1 }[/math]（[math]\displaystyle{ P=0 }[/math]）。

这里我们用了记号[math]\displaystyle{ \bar{P} }[/math]来表示把一个逻辑变量（布尔逻辑二值变量，取值为0或者1）[math]\displaystyle{ P }[/math]的值反过来的操作，也就是如果[math]\displaystyle{ P=1 }[/math]，则[math]\displaystyle{ \bar{P}=0 }[/math]，如果[math]\displaystyle{ P=0 }[/math]，则[math]\displaystyle{ \bar{P}=1 }[/math]。

概念地图

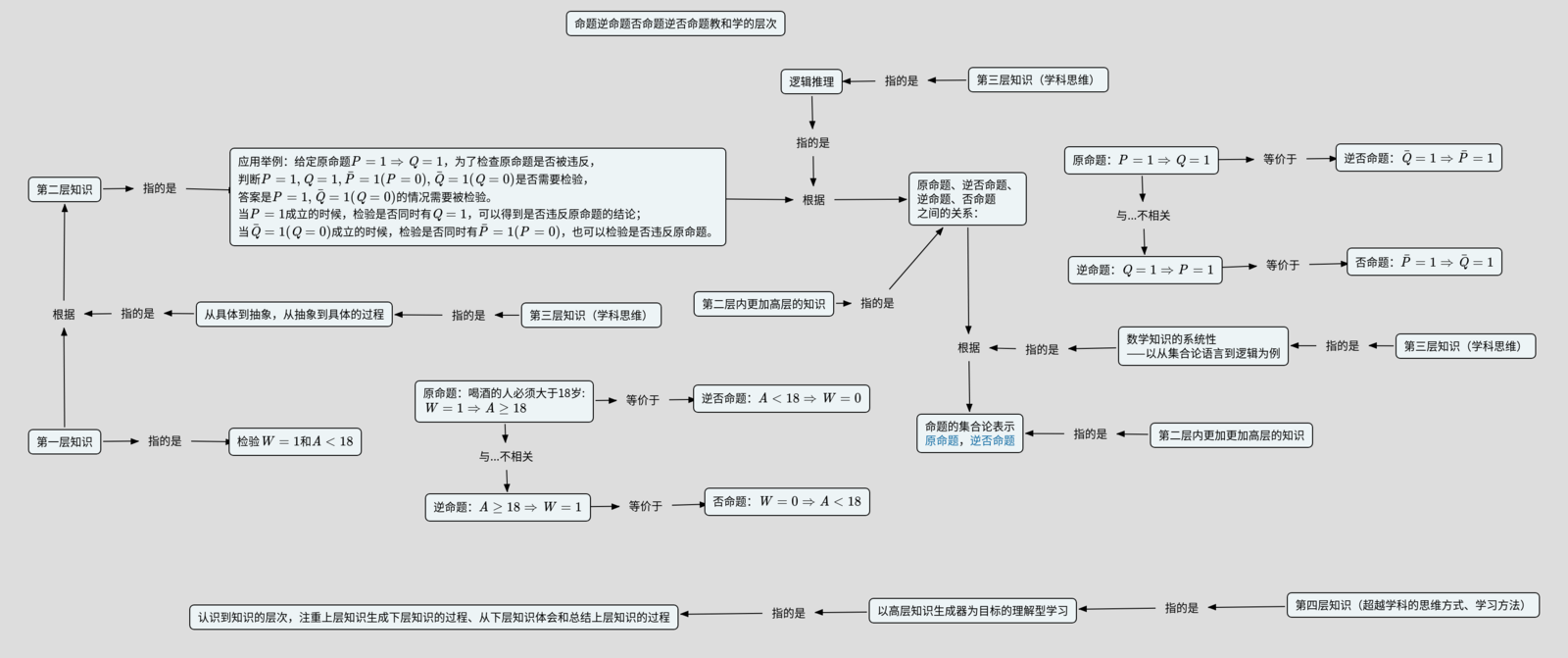
乘法的概念地图（图的格式将来改成嵌入文本的格式，用户既可以直接下载图，还可以获取这个概念地图的文本文件）：

教和学的层次

在定理和逆否定理的关系的教学中，如果主要任务就是让学生记住和会在简单的接近生活的实际场景中运用“定理和逆否定理等价”，则属于第一层教和学——事实性和流程性知识的教和学。例如，在上面的概念地图中，我们用具体的“喝酒的人的年龄必须大于等于18岁”为例，展示了其等价的描述“年龄小于18岁的不能喝酒”。并且，在这个例子上，我们编了一个问题来解决一下，“如果你可以选择是否对某个人做有没有违反这个规定的检查，你是否会检查：12岁的人，22岁的人，喝酒的人，喝绿茶的人”。

一旦，我们从这个具体例子，走到更加一般的条件[math]\displaystyle{ P,Q }[/math]的语言，也就是喝酒年龄问题背后的数学概念，则基于这样的从具体到抽象，从抽象到具体的过程的教和学，就是第二层次的教和学。更进一步，可以问这个抽象语言[math]\displaystyle{ P,Q }[/math]表达的定理和逆否定理等价怎么就能够回答要检测什么的问题。这也是第二层次的教和学，不过是用同层次内更加高层的知识来理解同层次内相对浅层的知识。乃至于，再进一步，我们可以追问为什么原定理和逆否定理会等价，然后用集合论的语言来证明和理解这个等价性，这也是第二层次的教和学，不过就是用同一层次内更加高层的知识来理解同层次内相对浅层的知识。

不过，跳出这个具体知识，我们看到，从集合论的语言到原命题和逆否命题的等价性，从原命题和逆否命题的等价性来做出来如何检测的选择，分别反映了“数学知识的系统性”、“逻辑推理是数学论证的重要形式，数学需要讲究论证”，这些关于数学的学科大图景的内容。这就属于第三个层次的知识。

再进一步，数学论证反映了批判性思维，从知识生成的过程来理解知识反映了理解型学习，这些超越具体学科的一般思维方式和学习方法，这属于第四个层次的知识。

中小学阶段的理解

至少要达到具象层面的第二层的理解，也就是用具体例子的语言来体会到“原定理和逆否定理”的等价性。如果进一步到抽象层面的第二层就更好了，也就是可以用抽象语言的“原定理和逆否定理”来看到一类具体问题背后的相同的逻辑。

尽量达到第三层的理解，也就是从这些例子体会到数学论证、数学知识的系统性。

如果还能够走到第四层，也就是数学概念的学习需要依靠系联性思考、批判性思维、以知识生成器为目标的理解型学习，那就更好了。