定义和含义

直角三角形长边对大角定理，指的是，在直角三角形中，对于两个直角边来说，较长的直角边边总是对着两个锐角中较大的那个角。

层次标注

在这里，它属于第二层知识，即学科概念。

辅助理解的解释

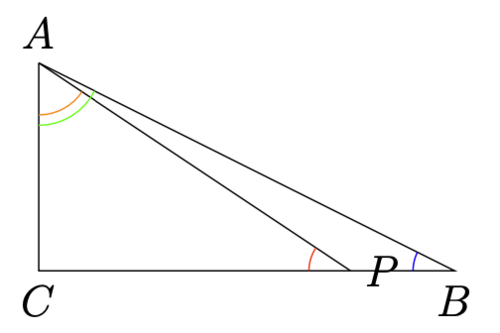
(图片来源于《小学数学这样学》^[1])

这里，我们用图中的例子来具体说明，就是在直角三角形 [math]\displaystyle{ \triangle A B C }[/math] 中, 以点 [math]\displaystyle{ A }[/math] 为顶点, 选取 [math]\displaystyle{ C B }[/math] 上一点 [math]\displaystyle{ P }[/math] , 连接 [math]\displaystyle{ A P }[/math] , 得到的一个新的直角三角形 [math]\displaystyle{ \triangle A C P }[/math] 。如果 [math]\displaystyle{ P }[/math] 在 [math]\displaystyle{ B, C }[/math] 之间则 [math]\displaystyle{ \angle C A P\lt \angle C A B }[/math] ; 同时，如果有 [math]\displaystyle{ \angle C A P\lt \angle C A B }[/math] , 则 [math]\displaystyle{ P }[/math] 在 [math]\displaystyle{ B, C }[/math] 之间。

对这个定理进行数学证明

这个定理的证明基于三角形内角和公理，三角形内角外角定理。 以下是摘自《小学数学这样学》的证明内容^[1]：

证明：图中 [math]\displaystyle{ P }[/math] 在 [math]\displaystyle{ B, C }[/math] 之间, 则按照外角大于不相邻的内角, 我们有:

按照三角形内角和等于 [math]\displaystyle{ 180^{\circ} }[/math] ，我们有:

合起来，我们有:

反过来，如果 [math]\displaystyle{ P }[/math] 在 [math]\displaystyle{ B C }[/math] 外侧 (射线 [math]\displaystyle{ C B }[/math] 上)，则 [math]\displaystyle{ \angle C A P\gt \angle C A B }[/math] 。 于是，如果已知 [math]\displaystyle{ \angle C A P\lt \angle C A B }[/math] 则 [math]\displaystyle{ P }[/math] 在 [math]\displaystyle{ B, C }[/math] 之间。 此外, 我们图中的三角形是直角 [math]\displaystyle{ \angle A C B }[/math] 在左侧, 锐角 [math]\displaystyle{ \angle A B C }[/math] 在右 侧。把图左右翻转一下，结论也是一样的。

从定理更进一步思考

从这个定理我们知道, 对于给定的直角三角形 [math]\displaystyle{ \triangle A B C }[/math] , 任何一条夹角 [math]\displaystyle{ \angle C A P\lt \angle C A B }[/math] 的射线，都不可能和 [math]\displaystyle{ B C }[/math] 平行，因为其必交 [math]\displaystyle{ B C }[/math] 于 [math]\displaystyle{ B, C }[/math] 之间的点 [math]\displaystyle{ P }[/math] 。也就是说, 如果要作一条经过 [math]\displaystyle{ A }[/math] 点的平行于 [math]\displaystyle{ B C }[/math] 的射线 [math]\displaystyle{ A P }[/math] ,则夹角 [math]\displaystyle{ \angle C A P\gt \angle C A B }[/math] 。等于也不行, 因为等于就会得到点 [math]\displaystyle{ P, B }[/math] 重合, 也就是射线 [math]\displaystyle{ A P }[/math] 交 [math]\displaystyle{ B C }[/math] 于 [math]\displaystyle{ B }[/math] ^[1]。

直觉上, 只要我们把直角三角形的 [math]\displaystyle{ \angle C A B }[/math] 不断地变大 (通过直角三角形长边对大角定理), 也就相当于要求 [math]\displaystyle{ \angle C A P }[/math] 不断地变大。那么, [math]\displaystyle{ \angle C A B }[/math] 最大能够多大呢? 不能大于 [math]\displaystyle{ 90^{\circ} }[/math] 。因为直角三角形的两个锐角内角之和是 [math]\displaystyle{ 180^{\circ}-90^{\circ}=90^{\circ} }[/math] 。也就是说, [math]\displaystyle{ \angle C A P }[/math] 可能得大于等于 [math]\displaystyle{ 90^{\circ} }[/math] 。但是, 另一方面, 当 [math]\displaystyle{ \angle C A P }[/math] 真的大于 [math]\displaystyle{ 90^{\circ} }[/math] 的时候, 我们 可以反向延长射线 [math]\displaystyle{ A P }[/math] 。类似地可以证明这个时候, 反向延长的射线 [math]\displaystyle{ A P }[/math] 会 和 [math]\displaystyle{ B C }[/math] 在另一侧相交。也就是 [math]\displaystyle{ A P }[/math] 不能平行于 [math]\displaystyle{ B C }[/math] 。于是, 看起来, [math]\displaystyle{ \angle C A P }[/math] 的最大值只能恰好取值 [math]\displaystyle{ 90^{\circ} }[/math] 。

我们在从三角形内角和到平行公理的证明中严格证明了上面的猜想。