定义和含义

平行公理，指的是，过给定的直线外给定的一个点有且只有一条直线和原直线平行，或者称为平行线唯一公理^[1]。

平行公理也可以表述为，[math]\displaystyle{ \text { 如果 } l_{1}\left\|l_{2}, l_{2}\right\| l_{3} \text {, 则 } l_{1} \| l_{3} }[/math]，或者称之为平行线传递公理^[1]。

平行公理是平面几何中非常重要的公理，构建了平面几何的基础。

层次标注

在这里，它属于第二层知识，即学科概念。

对这个定理的两种表述进行数学证明

以下是摘自《小学数学这样学》的证明内容^[1]：

从平行线唯一公理到平行线传递公理

证明基于直线交点数目定理和平行线唯一公理。

证明：我们假设平行没有传递性，也就是说, 已知 [math]\displaystyle{ l_{1}\left\|l_{2}, l_{2}\right\| l_{3} }[/math] , 但是 [math]\displaystyle{ l_{1} }[/math] 和 [math]\displaystyle{ l_{3} }[/math] 相交于一点 [math]\displaystyle{ P }[/math] (两条不同的直线, 不 平行就肯定相交)。

于是我们发现, 对于直线 [math]\displaystyle{ l_{2} }[/math] 来说, 过直线外一点 [math]\displaystyle{ P }[/math] 有两条直线和它平行, 这和平行线唯一公理表述矛盾。

于是, 假设错误, 也就是说, [math]\displaystyle{ l_{1} \| l_{3} }[/math] 。

从平行线传递公理到平行线唯一公理

证明使用反证法，基于平行线传递公理和直线交点数目定理。

证明： 我们先假设过直线外一点没有任何一条直线, 或者有两条或者两条以上的直线和给定直线平行。

首先, 没有肯定不对, 因为平行线传递公理的前提就是存在 [math]\displaystyle{ l_{1} \| l_{2} }[/math] 这样的平行关系。

接着, 我们来看两条或 者两条以上对不对。如果过 [math]\displaystyle{ l_{2} }[/math] 外一点 [math]\displaystyle{ P }[/math] 有两条直线 [math]\displaystyle{ l_{1}, l_{3} }[/math] 都和 [math]\displaystyle{ l_{2} }[/math] 平行, 则 [math]\displaystyle{ l_{1}, l_{3} }[/math] 相交于 [math]\displaystyle{ P }[/math] , 也就是不平行。

可是, 由于 [math]\displaystyle{ l_{1}\left\|l_{2}, l_{3}\right\| l_{2} }[/math] , 按照平行线传递公理 [math]\displaystyle{ l_{1} \| l_{3} }[/math] 不相交。矛盾。

因此, 假设错误, 也就是过直线外一点不可能存在两条或者两条以上的平行线。

从三角形内角和公理到平行线唯一公理

实际上，平行线唯一性公理和三角形内角和公理，我们只需要保留其中任意的一条，两者可以相互证明^[1]。

证明基于平行线性质定理、平角的含义。以下是摘自《小学数学这样学》的证明内容^[1]：

从三角形内角和公理到平行线唯一性公理

这个证明基于三角形内角和公理、直角三角形锐角可以取任意小定理、直角三角形长边对大角引理。

(图片来源于《小学数学这样学》^[1])

以下是摘自《小学数学这样学》的证明内容^[1]：

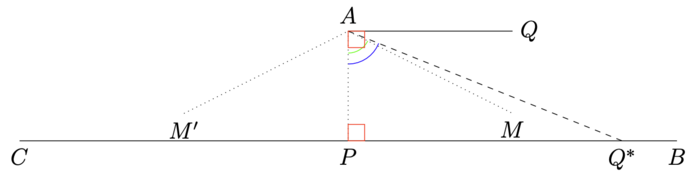
证明：如右图(从三角形内角和公理到平行公理)所示，我们先来作一条过直线外一点 [math]\displaystyle{ A }[/math] 平行于 [math]\displaystyle{ B C }[/math] 的平行线: 先作过直线外一点 [math]\displaystyle{ A }[/math] 的 [math]\displaystyle{ B C }[/math] 的垂线，垂线和 [math]\displaystyle{ B C }[/math] 的交点记作 [math]\displaystyle{ P }[/math] ; 然后, 我们再来作一条过直线上一点 [math]\displaystyle{ A }[/math] 垂直于 [math]\displaystyle{ A P }[/math] 的直线 [math]\displaystyle{ A Q }[/math] 。

有了这个图，我们来证明 [math]\displaystyle{ A Q \| C B }[/math] 。由于 [math]\displaystyle{ \angle A P B }[/math] 和 [math]\displaystyle{ \angle P A Q }[/math] 都是直角, 因此, 两者互补。对于直线 [math]\displaystyle{ A Q }[/math] 和 [math]\displaystyle{ C B }[/math] 而言, 这两个角度刚好就是同旁内角。同旁内角互补, 则直线平行。我们得到 [math]\displaystyle{ A Q \parallel C B }[/math] 。

现在，我们假设平行公理不成立，也就是说过直线外一点要么不存在 (已经被上面的作图过程否定) 任何一条平行线, 要么存在两条或者两条以上的平行线。现在，我们来证明存在两条平行线也是不可能的。 证明两条的情况以后, 两条以上就可以自然被否定。记这个第二条平行线为 [math]\displaystyle{ l }[/math] ——过 [math]\displaystyle{ A }[/math] 点, 指向不同于 [math]\displaystyle{ A Q }[/math] 的一条直线。

我们说, [math]\displaystyle{ l }[/math] 要么是图中左侧往下 [math]\displaystyle{ A M^{\prime} }[/math] 的方向, 要么是图中右侧往下 [math]\displaystyle{ A M }[/math] 的方向。如果既不是左侧往下，也不是右侧往下，则只能和 [math]\displaystyle{ A P }[/math] 垂直，也就是 [math]\displaystyle{ \angle P A M=\angle P A Q=90^{\circ} }[/math] 。于是，根据过直线上一点有且只有一条垂线, [math]\displaystyle{ l }[/math] 就是 [math]\displaystyle{ A Q }[/math] 。矛盾。也就是说 [math]\displaystyle{ \angle P A M \neq \angle P A Q= 90^{\circ} }[/math] 。

我们取出来其中一种情形 [math]\displaystyle{ A M }[/math] 来讨论。[math]\displaystyle{ A M^{\prime} }[/math] 的情形类似。注意, [math]\displaystyle{ A M \| C B }[/math] , 因此, [math]\displaystyle{ A M }[/math] 和 [math]\displaystyle{ C B }[/math] 没有交点。同时, 由于 [math]\displaystyle{ A M }[/math] 在右侧往下, 因此, [math]\displaystyle{ \angle P A M \lt \angle P A Q }[/math] (如果大于, 就自然成了 [math]\displaystyle{ A M^{\prime} }[/math] 的情形)。

根据直角三角形锐角可以取任意小定理, 当 [math]\displaystyle{ \angle P A M \lt \angle P A Q }[/math] 的时候, 我们总是可以找到一个直角三角形 [math]\displaystyle{ \triangle A P Q^{*} }[/math] ，其中 [math]\displaystyle{ Q^{*} }[/math] 在直线 [math]\displaystyle{ C B }[/math] 上)，使得 [math]\displaystyle{ \angle P A M \lt \angle P A Q^{*} }[/math] , 或者说反过来, 使得 [math]\displaystyle{ \angle Q A Q^{*} \lt \angle Q A M }[/math] 。

根据直角三角形长边对大角引理，我们知道小角对小边，也就是 [math]\displaystyle{ A M }[/math] 必定交 [math]\displaystyle{ B C }[/math] 于一点，而且这个点在 [math]\displaystyle{ P Q^{*} }[/math] 的内侧。这个结论和 [math]\displaystyle{ A M }[/math] 平行于 [math]\displaystyle{ B C }[/math] 矛盾。

因此，原假设错误，也就是过直线外一点 [math]\displaystyle{ A }[/math] 有且只有一条平行于 [math]\displaystyle{ B C }[/math] 的直线。

从平行线唯一性公理到三角形内角和公理

这个证明基于平行线性质定理。

(图片来源于《小学数学这样学》^[1])

以下是摘自《小学数学这样学》的证明内容^[1]：

证明：如图所示, 我们延长一下 [math]\displaystyle{ B C }[/math] 到 [math]\displaystyle{ D }[/math] 。根据平行公理, 存在着一条过三角形 [math]\displaystyle{ \triangle A B C }[/math] 的顶点 [math]\displaystyle{ C }[/math] 平行于 [math]\displaystyle{ A B }[/math] 的线 [math]\displaystyle{ C E }[/math] 。根据平行线的性质, 我们有内错角 [math]\displaystyle{ \angle E C A=\angle B A C }[/math] , 同位角 [math]\displaystyle{ \angle D C E= \angle C B A }[/math] 。于是, 三角形的内角和等于