分类:IOFactor微扰计算

IOFactor的定义是在投入产出矩阵[math]\displaystyle{ A }[/math]中去掉第[math]\displaystyle{ k }[/math]行和第[math]\displaystyle{ k }[/math]列得到[math]\displaystyle{ A^{\left(-k\right)} }[/math]，然后计算本征值和本征向量。每次重新开始计算本征值和本征向量比较耗资源。另外，还想从理论上看一下这个因子和PageRank等其他广义投入产出分析的指标的关系。于是，我们尝试了微扰计算。

[math]\displaystyle{ A^{\left(-k\right)}=A-\left|k\right\rangle\left\langle k \right|A-A\left|k\right\rangle\left\langle k \right| + \left|k\right\rangle\left\langle k \right|A\left|k\right\rangle\left\langle k \right| }[/math] 也就是 [math]\displaystyle{ \Delta A = -\left|k\right\rangle\left\langle k \right|A-A\left|k\right\rangle\left\langle k \right| + \left|k\right\rangle\left\langle k \right|A\left|k\right\rangle\left\langle k \right| }[/math]

于是，按照一级微扰论[math]\displaystyle{ \Delta \lambda = \frac{\left\langle v \right|\Delta A\left|u\right\rangle}{\left\langle v \right|\left.u\right\rangle} }[/math]，本征值的微扰等于（考虑到分母用到了PageRank值[math]\displaystyle{ \left\langle v \right|\left.u\right\rangle=1 }[/math]，可简单证明，见广义投入产出分析）

[math]\displaystyle{ \Delta \lambda = \left\langle v \right|\left[-\left|k\right\rangle\left\langle k \right|A-A\left|k\right\rangle\left\langle k \right| + \left|k\right\rangle\left\langle k \right|A\left|k\right\rangle\left\langle k \right|\right]\left|u\right\rangle }[/math] 其中，[math]\displaystyle{ \left\langle v \right| }[/math]和[math]\displaystyle{ \left|u\right\rangle }[/math]分别是[math]\displaystyle{ A }[/math]的本征值为[math]\displaystyle{ \lambda }[/math]的左右本征向量。 [math]\displaystyle{ \Delta \lambda = -v_{k}\left\langle k \right|A\left|u\right\rangle-\left\langle v \right|A\left|k\right\rangle u^{k} + v_{k}\left\langle k \right|A\left|k\right\rangle u^{k} = -v_{k}u^{k}-v_{k}u^{k} + v_{k}A^{k}_{k}u^{k} }[/math]

所以， [math]\displaystyle{ IOF_{k}=-\Delta \lambda = 2v_{k}u^{k}-v_{k}A^{k}_{k}u^{k}=\left( 2-A^{k}_{k}\right)v_{k}u^{k} }[/math]

这里的括号外面实际上是PageRank值。可以通过数值实验来检验一下。

[math]\displaystyle{ A^{\left(-k\right)}(|u\rangle+|\Delta u\rangle) = (\lambda + \Delta\lambda) (|u\rangle+|\Delta u\rangle) }[/math]

去掉k行k列后[math]\displaystyle{ \langle k|\Delta u\rangle=0 }[/math]，可以将[math]\displaystyle{ |\Delta u\rangle=|u\rangle + |\delta\rangle - u_k|k\rangle }[/math]

左乘[math]\displaystyle{ \langle v| }[/math]，忽略2阶小量，整理得到

[math]\displaystyle{ \Delta\lambda = \left(\langle v|\Delta A|u\rangle -\langle v|\Delta A|k\rangle \langle k|u\rangle\right)/(\langle v|u\rangle-\langle v|k\rangle\langle k|u\rangle) }[/math]

给定[math]\displaystyle{ \Delta A = -\left|k\right\rangle\left\langle k \right|A-A\left|k\right\rangle\left\langle k \right| + \left|k\right\rangle\left\langle k \right|A\left|k\right\rangle\left\langle k \right| }[/math] ,于是有

[math]\displaystyle{ \langle v|\Delta A|u\rangle=-v_{k}u^{k}-v_{k}u^{k} + v_{k}A^{k}_{k}u^{k} }[/math]

[math]\displaystyle{ \langle v|\Delta A|k\rangle \langle k|u\rangle=-v_ku^k }[/math]

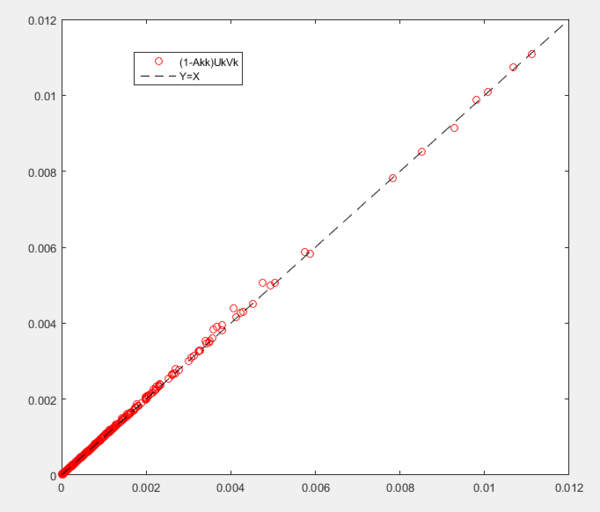
[math]\displaystyle{ IOF_k = -\Delta\lambda =(1-A^k_k)v_ku^k }[/math]

数值上的检验：