定义和含义

在数学运算中，当我们不再去关心具体的数，而是关心运算本身，这时候具体的数就不再重要，于是我们不妨用字母代替具体的数写在算式中。这时候，这些代替具体的数的字母，就称为代数。而这个过程中，就体现了代数的思想。

代数的思想，指的是用字母或者其他符号表示数(以及其他更加复杂的数学结构)，用运算符表示关系，这个用记号来辅助思考的功能。

用字母来表示数和算式，很多时候能够更好地体现一类算式的共同特征，也就是帮我们注意到和表达好从特殊到一般的联系。

辅助理解的解释

例如在 [math]\displaystyle{ 1+1=2 }[/math] 中，我们关心的是 [math]\displaystyle{ 1 }[/math] 加上 [math]\displaystyle{ 1 }[/math] 等于 [math]\displaystyle{ 2 }[/math] ，也就是 [math]\displaystyle{ 1 }[/math] 和 [math]\displaystyle{ 2 }[/math] 这些数。

而在 [math]\displaystyle{ a+b=c }[/math] 中，我们关心的是加法本身，而不是具体的数，因此就可以用 [math]\displaystyle{ a，b，c }[/math] 来代替 [math]\displaystyle{ 1+1=2 }[/math] 中的具体的数。这样用字母表示可以任意取值的数量。

这里的 [math]\displaystyle{ a，b，c }[/math] 的字母，就是代数。这里的 [math]\displaystyle{ a+b=c }[/math] 的式子，就是代数表达式。从具体的运算，到抽象的代数表达式，这个过程中就体现了代数的思想。这些都是数学成为思维的语言的基础。代数的思想是数学中非常重要而且常用的思维方式，毫不夸张的说，代数思想是迈入新的数学世界，即将起飞的起点。

一个例子来体会代数思想的威力：

桌子上的猫

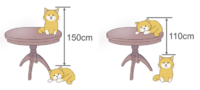
有两只完全一样的猫，还有一张桌子。左边是一只在地上趴着，一只在桌子上站着。右边是一只在地上站着，一只在桌子上趴着。我也不知道为什么，有人测量出来了两只猫之间的高度差。请你来算算桌子的高度。 我们用字母 [math]\displaystyle{ T }[/math] , [math]\displaystyle{ C_s }[/math] , [math]\displaystyle{ C_l }[/math] 分别表示桌子的高度、站着的猫的高度、趴着的猫的高度。注意，这里我们就用了字母来表示数，表示事物的量。我们再来看这些高度和测量出来的高度差之间的关系。我们发现，左边和右边分别是 [math]\displaystyle{ T+C_s-C_l = 150(厘米) }[/math] ,[math]\displaystyle{ T+C_l-C_s = 110(厘米) }[/math]

现在，我们把两个算式相加(请思考为什么可以把两个等式加起来)，得到[math]\displaystyle{ （T+C_s-C_l）+（T+C_l-C_s）=260（厘米） }[/math]， 因此 [math]\displaystyle{ T=130（厘米） }[/math]

我们发现，一旦我们去观察两个等式，注意到这两个等式之间的关系 —— [math]\displaystyle{ T+C_s-C_l }[/math] 和 [math]\displaystyle{ T+C_l-C_s }[/math] 的联系，就很容易发现，只要我们把两个等式相加，就可以去掉那些不知道是多少的 [math]\displaystyle{ C_s }[/math] , [math]\displaystyle{ C_l }[/math] 。这样的一个观察，如果我们没有代数的思想——用字母来代表数和算式，是完全不可能得到的。