问题背景

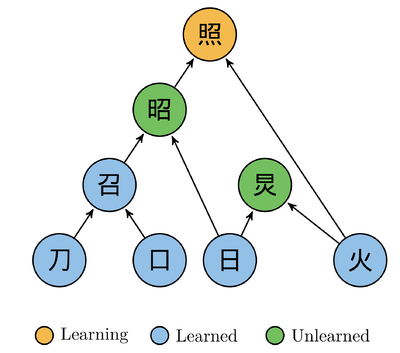
汉字之间是相互联系的。汉字可以一个个字单独地学习，也可以想办法运用汉字的联系来学习。例如，学习“林”的时候，如果已经学习过“木”，则可以通过“林就是很多树木长在一起形成的”来学习“林”。例如，“涉”就是通过“徒步（脚趾头，止）”跨越“河流，三点水”的意思。那么，是不是大多数汉字都可以这样来学习呢？是不是这样的学习确实会提高学习效率呢？

我们汉字学习的研究工作^[1] 就企图回答这几个问题。这是我们根据这个研究工作制作和发布的“汉字理解型学习网站http://www.learnm.org”。

汉字网络

首先，我们把每一个汉字根据其组成部分做一个直接的有意义的拆分。有意义的含义指的是读音上或者含以上，上层字和下层字之间能够建立联系。直接的意思就是，如果拆出来的下层字还可以再一次拆分，我们放在下一层来考虑它，在这一层把能够继续拆分的下层字当做一个整体来看。例如，

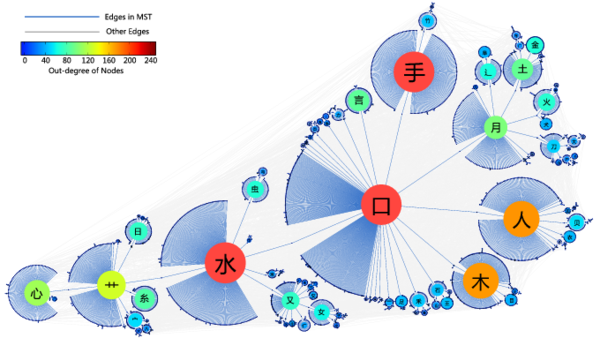
通过这样的拆分，我们得到3500常用汉字的地图，

如果你愿意还可以下载pdf格式的汉字地图文件:FullmapBig.pdf

注意，在汉字网络中，汉字构成的只有汉字，所以，所有的顶点都是字。在更一般的概念网络中，概念和概念合起来可以构成概念，还可以构成命题。因此，将会遇到两类顶点——概念和命题。

有了概念地图能够做什么？

地图实际上代表的是汉字和汉字之间的投入产出关系，把自己的形状含义和读音投入到更复杂的字之中去称为更复杂的字的形状含义和读音的一部分。

有了这个投入产出关系，汉字在语料库中的使用频率就是这个汉字的外生影响力。把这个影响力在汉字地图中——沿着汉字构成关系反向——做传播，就得到了汉字的综合影响力。一个复杂的汉字的使用频率的一部分可以传递到它的组成部分，也就是更简单的字上面，这样下面的汉字就会变得更重要。甚至当其自身的使用频率都不大的时候，这个传播得到的影响力，很可能也会比较大。同时，如果一个简单字参与了多个复杂字的构造，则每一个这样的复杂字都会把使用频率的一部分传到这个简单字上。这样这个简单字也会变成需要优先学习的字。并且，这个外生影响力，可以按照学习目的来概念，例如，针对儿童的语料来统计儿童使用汉字的频率，针对医学学科的汉字使用频率等等。

在用广义投入产出分析做汉字学习顺序的计算的时候，还可以考虑高级字对低级字的启发作用（学习了更复杂的汉字，也可以从一定程度上启发简单汉字的学习）。

有了这个地图，我们还可以来研究汉字检测的问题。如果一个被试不认识“木”我们可以很大可能推断其不认识“林”，或者反过来认识“林”则推断很大的可能认识“木”。这样就可以通过自适应地检测少数的汉字来诊断被试对所有汉字的认识与否。具体算法上，可以采用汉字分级加上上下级推断（底层汉字不认识则推断上层很高的可能也不认识，上层汉字认识则推断下层汉字有很高的可能认识），也可以把机器学习的更新算法——梯度反向传播——用来识别对于学习者来说收益最大成本最小的学习的点。

梯度反向传播算法用于推荐个性化学习和考试顺序

定义整体学习顺序[math]\displaystyle{ \vec{S}=\left[s_{1},\cdots, s_{i}=\mu, \cdots, s_{L}\right] }[/math]，其中[math]\displaystyle{ s_{i}=\mu }[/math]的含义就是把汉字[math]\displaystyle{ \mu }[/math]放到第[math]\displaystyle{ i }[/math]个来学习。考虑到更一般的情况，[math]\displaystyle{ L }[/math]不一定等于汉字总数[math]\displaystyle{ N }[/math]，学习者可以把学习到某个子集的汉字当做学习目标。

构建学习到第[math]\displaystyle{ l }[/math]个汉字的时候的收益函数，[math]\displaystyle{ E\left(l;\alpha\right)=\sum_{j=1}^{l}\left(\alpha s_{j}+s_{j}f_{j}\right) }[/math]和成本函数[math]\displaystyle{ C\left(l\right)=\sum_{j=1}^{l}\left(s_{j}c_{j}\left(s_{1}, \cdots, s_{j}\right)\right) }[/math]，其中[math]\displaystyle{ c_{j}\left(s_{1}, \cdots, s_{j}\right) }[/math]依赖于网络结构（稍后把这个学习成本函数改写成邻接矩阵的形式）。为简单计，可以仅仅考虑[math]\displaystyle{ l=L }[/math]。

这时候，我们就可以在学习顺序空间中通过机器学习来得到优化的学习顺序。当然，对学习顺序做梯度反向传播的优化仍然可能收敛到局域的最优点，而不一定是全局的最优点。

或者考虑贪心算法，每次仅仅选择一个当前看来收益比上成本最高的汉字来学习。当然，贪心算法不一定能够给出来整体上最高效的学习算法。整体高效的算法可能是具有前瞻性的，每个时刻都是考虑了多个汉字的学习顺序的。不过，一步的贪心算法容易实现很多。我们就来尝试一下一步的贪心算法。记当前所有汉字的学习状态为[math]\displaystyle{ \vec{x}\left(t\right)=\left[x_{1}\left(t\right),\cdots, x_{i}\left(t\right)= 1,0, \cdots, x_{N}\left(t\right)\right] }[/math]。其中[math]\displaystyle{ x_{i}\left(t\right)= 1 }[/math]（0）表示[math]\displaystyle{ i }[/math]这个字已经（没有）被学会。这个时候计算下一步学习任何一个新字的成本和收益为，[math]\displaystyle{ e\left(j,t;\alpha\right)=\alpha +f_{j} }[/math]和成本函数[math]\displaystyle{ c\left(j,t\right)=c_{j}\left(\vec{x}\left(t\right)\right) }[/math]。和整体学习顺序的优化算法相比，贪心算法不仅仅是局域的，而且是每一步仅仅考虑在原来的学习顺序的基础上选择一个字来学习的各种顺序中哪一种最优，而整体学习顺序最优算法的每一步调整可能意味着多个汉字的学习顺序的调整。

个性化的学习顺序的问题，用这样的语言，就转化成，在给定一个当前学习状态[math]\displaystyle{ \vec{x}\left(\tau\right) }[/math]的基础上，对于还没有学会的汉字或者这些汉字中的一部分（记为汉字集合[math]\displaystyle{ \mathcal{N}\left(\tau\right)=\left\{1,\cdots, \theta, \cdots, \Theta_{\tau}\right\} }[/math]）来说，用什么样的学习顺序（记为[math]\displaystyle{ \vec{S}\left(\tau\right)=\left[s_{1},\cdots, s_{i}=\theta, \cdots, s_{\Theta_{\tau}}\right] }[/math]）是最优的。这个时候的收益函数是[math]\displaystyle{ E\left(\tau;\alpha\right)=\sum_{j=1}^{\Theta_{\tau}}\left(\alpha s_{j}+s_{j}f_{j}\right) }[/math]和成本函数[math]\displaystyle{ C\left(\tau\right)=\sum_{j=1}^{\Theta_{\tau}}\left(s_{j}c_{j}\left(\vec{x}\left(\tau\right), s_{1}, \cdots, s_{j}\right)\right) }[/math]，其中[math]\displaystyle{ \vec{x}\left(\tau\right) }[/math]指的是在[math]\displaystyle{ \tau }[/math]时刻已经学会的汉字。

类似地，也可以用贪心算法来处理这个个性化学习的问题。

现在，更有意思的问题来了：能不能用梯度反向传播算法找出来[math]\displaystyle{ \tau }[/math]时刻的学习者最高效的学习顺序，而不依赖于仅仅考虑一步的贪心算法以及上面的整体剩余汉字学习顺序的优化？也就是把机器学习算法真的用在汉字网络上，计算汉字网络上的成本和收益的梯度反向传播，从而推荐最好的更新方向。

如果这个问题能够解决，注意这里机器学习不再是对学习顺序空间的搜索了，而是真的运用汉字网络来计算梯度，那么，我们还可以把这个算法用于汉字高效检测，只不过收益函数和成本函数变化一下，但是，也在真实的汉字网络上做梯度反向传播计算来识别出来能够获取最多信息的下一步要检测的汉字。

学习成本的递归定义和显式定义

[math]\displaystyle{ c_{j}\left(s_{1}, \cdots, s_{j}\right) }[/math]指的是在学习了[math]\displaystyle{ \left(s_{1}, \cdots, s_{j-1}\right) }[/math]之后，下一步学习[math]\displaystyle{ s_{j} }[/math]的成本。定义汉字学习状态[math]\displaystyle{ x_{\mu}=\sum_{l=1}^{j-1}\delta_{s_{l},\mu} }[/math]表示，如果之前曾经有某一个[math]\displaystyle{ s_{l}=\mu }[/math]则这个汉字[math]\displaystyle{ \mu }[/math]已经被学习，则[math]\displaystyle{ x_{\mu}=1 }[/math]，否则[math]\displaystyle{ x_{\mu}=0 }[/math]。[math]\displaystyle{ \delta_{s_{l},\mu} }[/math]是Kronecker[math]\displaystyle{ \delta }[/math]记号：角标相同的时候等于1否则等于0。

递归定义学习成本[math]\displaystyle{ c_{j}\left(\vec{x}\right) = \sum_{k} A^{k}_{j}c_{k}\left(\vec{x}\right)\left(1-x_{k}\right)+cf_{j}\left(1-x_{j}\right) }[/math]。其中[math]\displaystyle{ A^{k}_{j} }[/math]表示汉字[math]\displaystyle{ k }[/math]是汉字[math]\displaystyle{ j }[/math]的一部分。[math]\displaystyle{ \left(1-x_{k}\right) }[/math]表示汉字[math]\displaystyle{ k }[/math]在当前没有被学习过。[math]\displaystyle{ \left(1-x_{j}\right) }[/math]表示汉字[math]\displaystyle{ j }[/math]在当前没有被学习过。合起来上面的公式表示，如果汉字[math]\displaystyle{ j }[/math]在当前没有被学习过，而我们现在要来学习，则先有一个部分学习成本是汉字[math]\displaystyle{ j }[/math]依赖于它的底层汉字而来的学习成本，还有一部分是这个字就算在所有底层汉字都已经学习过的前提下的学习难度。前者类似于概念同化之前的前置概念的成本，后者类似于本概念的概念形成和概念同化过程成本。

对于前者，如果这个底层汉字还是没有学习过的，也就是[math]\displaystyle{ \left(1-x_{k}\right)=1 }[/math]的，则我们还需要去递归计算这个汉字[math]\displaystyle{ k }[/math]的学习成本。这也就是前置概念学习成本。

一种概念形成成本的计算方式是[math]\displaystyle{ cf_{j}=\beta\sum_{k}A^{k}_{j} }[/math]，也就是这个汉字[math]\displaystyle{ j }[/math]有多少个部分，则其本概念学习难度就增加多少。

合起来，我们就有了学习成本递归计算公式：[math]\displaystyle{ c_{j}\left(\vec{x}\right) = \sum_{k} A^{k}_{j}c_{k}\left(\vec{x}\right)\left(1-x_{k}\right)+ \sum_{k}\beta\sum_{k}A^{k}_{j}\left(1-x_{j}\right) }[/math]。

那么，能不能把这个递归公式显示写出来，让方程的右边不再包含[math]\displaystyle{ c_{k}\left(\vec{x}\right) }[/math]呢？可以：[math]\displaystyle{ c_{j}\left(\vec{x}\right) = cf_{j}\left(1-x_{j}\right)+ \sum_{k_{1}} A^{k_{1}}_{j}cf_{k_{1}}\left(1-x_{k_{1}}\right)+\sum_{k_{1},k_{2}} A^{k_{1}}_{j}A^{k_{2}}_{k_{1}}cf_{k_{2}}\left(1-x_{k_{1}}\right)\left(1-x_{k_{2}}\right)+\cdots }[/math]，写成矩阵形式就是，[math]\displaystyle{ c\left(\vec{x}\right) = \left(1-X\right)cf + A\left(1-X\right)cf+A\left(1-X\right)A\left(1-X\right)cf+\cdots = \left[\left(1-A\left(1-X\right)\right)^{-1}-X\right]cf }[/math]。其中矩阵[math]\displaystyle{ X^{k}_{m}=x_{k}\delta_{km} }[/math]是一个对角矩阵，就是把状态矢量[math]\displaystyle{ x_{k} }[/math]放到对角线上，[math]\displaystyle{ X=diagonal\left(x\right) }[/math]。

有了这个当前时刻的成本计算公式，结合收益公式[math]\displaystyle{ e\left(j,\vec{x}\right)=f_{j}+\alpha }[/math]，我们就可以直接计算贪心算法的最优值，例如通过比较收益成本比：[math]\displaystyle{ \frac{e\left(j,\vec{x}\right)}{c_{j}\left(\vec{x}\right)} }[/math]。

不过，仅仅考虑一步的贪心算法是非常有局限的，真的计算还需要考虑针对整个学习顺序的优化，这个时候，我们需要的是整体学习顺序的学习成本，也就是[math]\displaystyle{ C\left(\vec{S}\right) = \sum_{j=1}^{L}\left\langle j \right\bar \left[\left(1-A\left(1-X\left(j-1\right)\right)\right)^{-1}-X\left(j-1\right)\right]cf }[/math]。这样的计算在实现上肯定没有递归计算来的快。因此，上面这个成本的显式公式主要在理论上可能有点作用，在实现上意义有限。

更多信息，请参阅^[1] 。

汉字拆分资源

汉字理解型学习网站：www.learnm.org

汉字全息系统：http://qxk.bnu.edu.cn/gjqxknew/jump/index

字频统计资源

按照汉语母语儿童口语、汉语母语儿童书面语（或者口语和书面语合起来）、汉语母语口语、汉语母语平衡语料；国外汉语学习者当地儿童口语、国外汉语学习者当地儿童书面语；国外汉语学习者当地口语、国外汉语学习者当地平衡语料，等不同方式来做字频统计。然后，在初学汉语的阶段依靠口语（对于儿童则采用儿童口语）的字频统计，在后续学习阶段采用平衡语料库的字频统计的方式来决定汉字学习顺序。

现代汉语语料库　https://www.corpus4u.org/　（字频词频文件下载）http://corpus.zhonghuayuwen.org/　（通过检索可以得到每个字的频率）

Combined character frequency list of Classical and Modern Chinese 汉字单字字频总表　http://lingua.mtsu.edu/chinese-computing/statistics/char/list.php?Which=TO

Academia Sinica Balanced Corpus of Modern Chinese http://www.sinica.edu.tw/SinicaCorpus/

Peking University Modern Chinese Corpus http://ccl.pku.edu.cn/ccl_corpus/xiandaihanyu/

Xiamen University corpora (registration required but free) http://www.luweixmu.cn/home/html/Corpora/

Beijing Language and Culture University corpus http://202.112.195.8

Lancaster Corpus of Mandarin Chinese http://bowland-files.lancs.ac.uk/corplang/cgi-bin/conc.pl

Leeds Chinese corpus http://corpus.leeds.ac.uk/query-zh.html

PFR People's Daily corpus (01/1998) http://bowland-files.lancs.ac.uk/corplang/pdcorpus/pdcorpus.htm

PH corpus (Xinhua newswire data 1990-1991) http://bowland-files.lancs.ac.uk/corplang/phcorpus/phcorpus.htm

People's Daily 2000 corpus http://bowland-files.lancs.ac.uk/corplang/pdc2000/default.htm

Peking University Ancient Chinese Corpus http://ccl.pku.edu.cn/ccl_corpus/jsearch/index.jsp?dir=gudai

Sinica corpus of early Chinese http://www.sinica.edu.tw/Early_Mandarin/

Sheffield Corpus of Chinese for Diachronic Linguistic Study http://www.shef.ac.uk/scc/

实用项目

概念网络建立好、学习顺序和诊断性检测的算法研究清楚、学习和检测实验验证了效果之后，就可以来做实用项目的开发和推广。

1. 首先，是以实验性学习材料和学习顺序、概念地图为基础，编撰学习材料
2. 接着，有了学习材料可以做教学培训和推广，以及实践研究
3. 然后，还可以从某些学科做起，逐渐推广到各个学科
4. 中间，可以开发一个小产品，当做本科创业项目：概念卡片
5. 最后，除了这些基本公益性质的学习材料和培训，还可以开展个性化学习顺序指导、个性化诊断性监测服务，甚至将来用这样的诊断代替考试
6. 顺便，在学习材料编撰上，也可以结合科学学研究，找出来和现在研究前沿相联系的学科基础概念，采用来自于研究工作以及其他学习材料的例子，来做学习材料的自动生成

概念卡片（以汉字为例）

以汉字为例，每一张卡片上是一个汉字的数据。正面包含：汉字字形、读音、网站链接和网站logo，反面包含：汉字拆分、理据性解释、古代字形、使用频率排序、分布式顶点权排序；中英文两个版本。

这实际上就是网站信息的卡片版本。尽管长远来看，肯定是网站和App更好。但是，目前阶段，卡片具有自己的优势，尤其是对于小孩的学习来说。

还可以考虑出三个版本，入门（最先学习的200字）版本、全完版（3500字）、高级版（9000字）。对于学生是学习资源，对于老师是教学资源。这个卡片包附一张原理和使用说明文件、一张汉字大图。

卡片可以是纸板、塑胶、木材、竹材等多种，可以分成多卷来卖。每张卡片，也就是每个概念，还可以配一个视频解说的小文件。

将来，可以把一般的概念也这样做出来。例如，小学阶段的数学已经做完概念地图和拆分，可以同样做出来。比如说，正面写“加法”，反面写“合起来数一数”，以及有关加法的局部概念地图。

教材编撰

1. 教学目标：系联性思考、培养思维深度、看得懂有东西可看愿意看、说得明白有东西可说愿意说
2. 整体设计原则：汉字学习顺序科学化、用篇章通过重复之前已经学习过的汉字来学习新的汉字、汉语拼音的学习弱化只需要将来能够用来输入汉字和正音即可、三年级之前主要解决识字问题、三年级以后主要教WHWM分析性阅读和写作以及分析和综合

可以参考戴汝潜《大成全语文》^[2]和这个帖子推荐戴汝潜《大成全语文》。

汉语字词难度测量和篇章阅读难度测量分级

考虑汉语字词的使用频率、读音透明性（一个字词的读音是否可以根据拆分结构读出来，或者说联系明显）、含义透明性（一个字词的含义是否可以根据拆分结构看出来，或者说联系明显）、字词子结构数量（汉语可以是笔画数、构成这个字的汉字的数量）、笔画数、相近字词数量，可以得到字词的难度测量模型，甚至做实验验证。见字词难度测量。

有了字词的难度度量，我们还可以通过考虑篇章的字词数量、句子数量、平均句子长度、平均字词难度等指标，以及篇章的内在逻辑难度来度量篇章的阅读难度，见阅读分级。

接着做一个结合了难度（成本）和频率（目标）的更进一步的学习顺序和检测方法。

其他语言的拆分和学习

参考文献