COVID-19 Time-Varying Reproduction Numbers on Global
这里有这个页面的中文版 新冠肺炎各国再生数。
Background and Motivation
Currently, COVID-19 has become a global scale threat to our health. Meanwhile, the situation in some regions such as China and Singapore has more or less become stable. To help everyone to be more aware of the global situation, and even hopefully contribute our possibly 3 cents to the intervention of this epidemics, we here calculated the time-varying reproduction number from time series of case numbers in each region on which we can get data and share it on this website. We will update daily when possible.
The basic reproduction number [math]\displaystyle{ R_{0} }[/math], which means roughly the number of new individuals will be infected on average by a single infector when there is no intervention at all, and the corresponding time-varying reproduction number [math]\displaystyle{ R\left(t\right) }[/math] at time [math]\displaystyle{ t }[/math] with possibly some interventions, are two important indicators of how severe is the epidemics and how effective are the interventions.
Here, we will provide first a time series of [math]\displaystyle{ R\left(t\right) }[/math] for each region on which we get data, and we will also show some predictive results based on very simple and rough extensions, which will be explained in the following.
Methods
While working on analysis of COVID-19 data, we note that the effective time-varing reproduction number of imported cases ([math]\displaystyle{ R_{0}^{1}\left(t\right) }[/math]) can be very different from the one of local cases ([math]\displaystyle{ R_{1+}^{2+}\left(t\right) }[/math]) due to the different intervention policy for imported cases and local cases. Thus, we
- classfifed all cases into the imported cases (the zeroth generation)[math]\displaystyle{ I^{0}\left(t\right) }[/math], locals infected by the imported cases (first generation) [math]\displaystyle{ I^{1}\left(t\right) }[/math] and locals infected by locals (second generation and beyond) [math]\displaystyle{ I^{2+}\left(t\right) }[/math],
- derived formulea calculating [math]\displaystyle{ R_{0}^{1}\left(t\right), R_{1+}^{2+}\left(t\right) }[/math] from time series of [math]\displaystyle{ I^{0}\left(t\right), I^{1}\left(t\right), I^{2+}\left(t\right) }[/math],
- Modified the R software EpiEstim according to the newly derived formulea.
Also, the test version of the modified EpiEstim has been provided at Github, and the manuscript on this new calculation will soon be posted on an arXiv website.
With the calculated [math]\displaystyle{ R\left(t\right) }[/math], we constructed two simple and rough scenarios to make some prediction,
- Null Scenario: extend the [math]\displaystyle{ R\left(t\right) }[/math] of a region of interest by taking [math]\displaystyle{ R\left(t\gt t_{end}\right)=R\left(t\gt t_{end}\right) }[/math], where [math]\displaystyle{ t_{end} }[/math] is the latest time of the known [math]\displaystyle{ R\left(t\right) }[/math], that is to say just take the latest value to be the future value of the time-varying reproduction number of a region of interest,
- Typical-Region Scenario: Extend the [math]\displaystyle{ R\left(t\right) }[/math] of a region of interest by connecting to it the [math]\displaystyle{ R_{typical}\left(t\right) }[/math] of a chosen typical region, which we use China (cn) and Singapore (sg).
[math]\displaystyle{ R\left(t\right) }[/math] of the two typical regions are decreasing functions since there is no data at the very beginning, and when there are data, usually there are interventions already.
When we connect for example [math]\displaystyle{ R_{cn}\left(t\right) }[/math] to [math]\displaystyle{ R\left(t\right) }[/math] of a region of interest, we might encouter three cases. Firstly, if the latest value [math]\displaystyle{ R\left(t_{end}\right) }[/math] is smaller than some values but at all values of [math]\displaystyle{ R_{cn}\left(t\right) }[/math], we find the place [math]\displaystyle{ t_{0} }[/math] such that [math]\displaystyle{ R_{cn}\left(t_{0}\right)=R\left(t_{end}\right) }[/math] and then let [math]\displaystyle{ R\left(t_{end}+t\right)=R_{cn}\left(t_{0}+t\right) }[/math]. Secondly, if the latest value [math]\displaystyle{ R\left(t_{end}\right) }[/math] is larger than all values of [math]\displaystyle{ R_{cn}\left(t\right) }[/math], we left extrapolate [math]\displaystyle{ R_{cn}\left(t\right) }[/math] (for example using the splinefun R function) so that we will find a large enough value such that [math]\displaystyle{ R_{cn}\left(t_{0}\right)=R\left(t_{end}\right) }[/math] (here [math]\displaystyle{ t_{0}\lt 0 }[/math]) and then again we let [math]\displaystyle{ R\left(t_{end}+t\right)=R_{cn}\left(t_{0}+t\right) }[/math]. Lastly, in principle, there is a case where [math]\displaystyle{ R\left(t_{end}\right) }[/math] is smaller than all [math]\displaystyle{ R_{cn}\left(t\right) }[/math], but we have not see such a cases in real data.
The Null Scenario is like to ask that if nothing changes what will happen, while the Typical-Region Scenario is to ask when will happen if the region of interest learn from the typical regions and those learned interventions are exactly as effective as they were in the original region.
There are some limitations of the method. First, the scenarios are too simple to be realistic. Second, in many other regions, due to data limitations, we have not distinguished the zeroth, first, second and beyond generations of cases. The method is currently applied to a single-region model, where all the other regions are treated as exogenous variables. In principle, the method is readily applicable to a multi-region situation, where flows among the regions can be estimated via traffic data.
Appendex to the methods section: some core formulea
If you are interested in knowing more about our analysis before we publish the paper, here are some core formulea:
- Locals infected by imported cases from some specific regions [math]\displaystyle{ I^{1}\left(t\right)=\sum_{\tau=0}^{\infty}I^{0}\left(t-\tau\right)R_{0}^{1}\left(t\right)\omega\left(\tau\right) }[/math], where the zeroth generation refers to the imported cases and locals infected by them are called the first generation
- Locals infected by local infectors, which themselves can be from the first generation or beyond [math]\displaystyle{ I^{2+}\left(t\right)=\sum_{\tau=0}^{\infty}\left(I^{1}\left(t-\tau\right)+I^{2+}\left(t-\tau\right)\right)R_{1+}^{2+}\left(t\right)w\left(\tau\right) }[/math], which we call the second generation and beyond
Correspondingly the time-varying reproducton numbers are respectively,
- [math]\displaystyle{ R_{0}^{1}\left(t\right)=\frac{I^{1}\left(t\right)}{\sum_{\tau=0}^{\infty}I^{0}\left(t-\tau\right)\omega\left(\tau\right)} }[/math]
- [math]\displaystyle{ R_{1+}^{2+}\left(t\right)=\frac{I^{2+}\left(t\right)}{\sum_{\tau=0}^{\infty}\left[I^{1}\left(t-\tau\right)+I^{2+}\left(t-\tau\right)\right]w\left(\tau\right)} }[/math]
Time-varying reproduction number of typical regions
Here we choose China except Hubei, which is simply due to the lack of data at the beginning of COVID-19 in Hubei, and Singapore as the typical regions as things are more or less under control now in those regions, and also we have a relatively long time series for those regions. Since they will be used as the basis of prediction scenario, here we first show their time-varying reproduction numbers.
Typical region I: China except Hubei
As we mentioned earlier, we classified cases into the imported cases, the locals infected by the imported cases, and the locals infected by the locals, and we estimate the [math]\displaystyle{ R_{0}^{1}\left(t\right) }[/math] and [math]\displaystyle{ R_{1+}^{2+}\left(t\right) }[/math].
The time-varying reproduction number of China except Hubei, [math]\displaystyle{ R_{0}^{1}\left(t\right) }[/math] and [math]\displaystyle{ R_{1+}^{2+}\left(t\right) }[/math] are calculated saperately. Later, we will only make use of [math]\displaystyle{ R_{1+}^{2+}\left(t\right) }[/math], the blue line. We can see that it starts from large than 2.5 and it reaches less than 0.5 very quickly.
The time-varying reproduction number of China except Hubei, combined [math]\displaystyle{ R\left(t\right) }[/math].
We should note that the combined [math]\displaystyle{ R\left(t\right) }[/math] is very different from the saperated [math]\displaystyle{ R_{0}^{1}\left(t\right) }[/math] and [math]\displaystyle{ R_{1+}^{2+}\left(t\right) }[/math].
Please contact us "the Safety Science and Complex System Team" if you want to make use of the data behind this analysis.
Typical region II: Singapore
The time-varying reproduction number of Singapore. Due to the lack of better data, we only calculated the combined [math]\displaystyle{ R\left(t\right) }[/math]. We can see it stars from a little over 2 and it reaches gradually to close to 0.5.
Time-varying reproduction number and some simple prediction of daily cases of some regions
In this section, we will show the calculated time-varying reproduction number [math]\displaystyle{ R\left(t\right) }[/math] of some regions. Again due to the lack of better data, we only calculated the combined [math]\displaystyle{ R\left(t\right) }[/math] of both imported and local infectors. Based on the calculated [math]\displaystyle{ R\left(t\right) }[/math] and the above known [math]\displaystyle{ R_{typical}\left(t\right) }[/math] of the typical regions, we also made some simple prediction of daily cases of those regions.
Japen
Time-varying reproduction number of Jappen
Time-varying reproduction number of Jappen, the combined [math]\displaystyle{ R\left(t\right) }[/math]
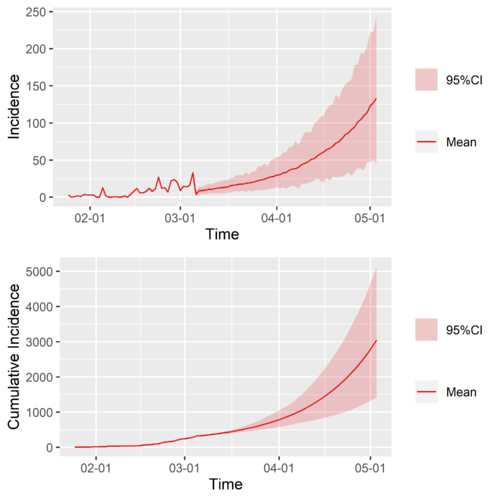
Predictions of Japen: Null Scenario
Null Scenario predictions of Japan. If the time-varying reproduction number of Jappen stays the same, this is what will happen.
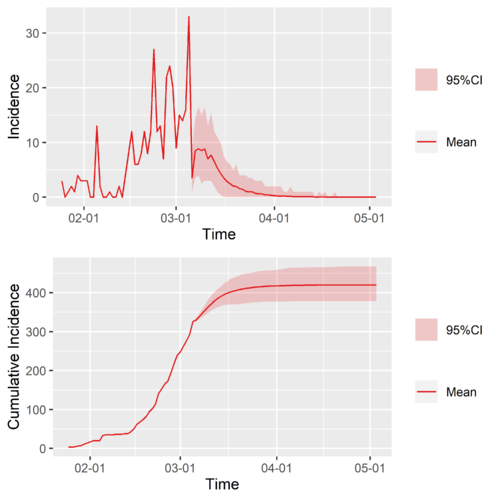
Predictions of Japan: Typical-region Scenario
Typical-Region scenario predictions of Japen, based on China except Hubei. If the time-varying reproduction number of Jappen take the track of the one of China except Hubei, this is what will happen.
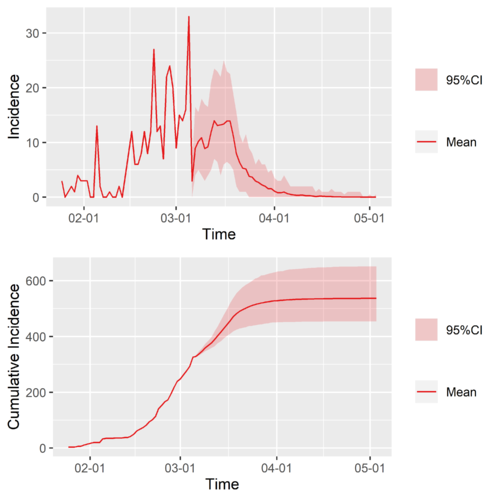
Typical-Region scenario predictions of Japan, based on Singapore. If the time-varying reproduction number of Jappen take the track of the one of Singapore, this is what will happen.
![The time-varying reproduction number of China except Hubei, [math]\displaystyle{ R_{0}^{1}\left(t\right) }[/math] and [math]\displaystyle{ R_{1+}^{2+}\left(t\right) }[/math] are calculated saperately.](/images/thumb/d/db/COVIDR.png/500px-COVIDR.png)
![The time-varying reproduction number of China except Hubei, combined [math]\displaystyle{ R\left(t\right) }[/math].](/images/thumb/8/88/COVIDR2.png/500px-COVIDR2.png)
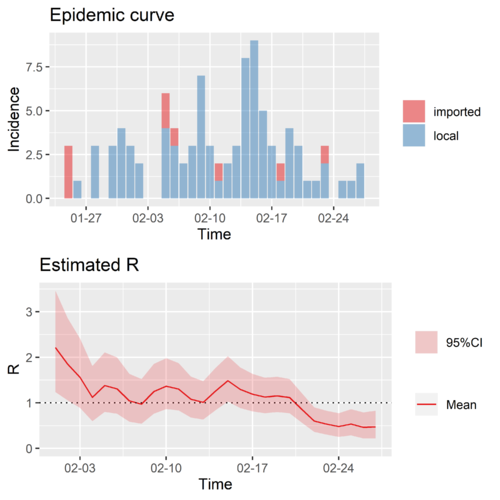
![Time-varying reproduction number of Jappen, the combined [math]\displaystyle{ R\left(t\right) }[/math]](/images/thumb/a/a0/Japan_R.png/500px-Japan_R.png)