分类:比较两个集合的方法
Title: Large enough sample size to rank two groups of data reliably according to their means
Authors: Zhesi Shen, Liying Yang, Zengru Di, Jinshan Wu
Abstract:
Often we need to compare two sets of data, say X and Y, and often via comparing their means 𝜇𝑋 and 𝜇𝑌 . However, when two sets are highly overlapped (say for example 𝜎2𝑋+𝜎2𝑌‾‾‾‾‾‾‾‾√≫|𝜇𝑋−𝜇𝑌| ), ranking the two sets according to their means might not be reliable. Based on the observation that replacing the one-by-one comparison, where we take one sample from each set at a time and compare the two samples, with the 𝐾𝑋 -by- 𝐾𝑌 comparison, where we take 𝐾𝑋 samples {𝑥1,𝑥2,…,𝑥𝐾𝑋} from one set and 𝐾𝑌 samples {𝑦1,𝑦2,…,𝑦𝐾𝑋} from the other set at a time and compare the averages ∑𝐾𝑋𝑗=1𝑥𝑗𝐾𝑋 and ∑𝐾𝑌𝑗=1𝑦𝑗𝐾𝑌 , reduces the overlap and thus improves the reliability, we propose a definition of the minimum representative size 𝜅 of each set for comparing sets by requiring roughly speaking 𝜎2𝐾𝑋+𝜎2𝐾𝑌‾‾‾‾‾‾‾‾‾‾√≪|𝜇𝑋−𝜇𝑌| ). Applied to journal comparison, this minimum representative size 𝜅 might be used as a complementary index to the journal impact factor (JIF) to indicate a measure of reliability of comparing two journals using their JIFs. Generally, this idea of minimum representative size can be used when any two sets of data with overlapping distributions are compared.
Keywords: Journal impact factor Minimum representative size Bootstrap sampling
这是对我们最近的一个关于统计学的工作[1],以及相关的工作[2]的总结。
问题背景
我们经常需要来对比包含多个元素的集合,例如比较两个研究机构甚至研究者在研究上的表现、对比不同学生的实际上包含了多道考题的考试成绩,甚至对比两个国家的民众的科学素养、身高等等。实际上,我们通常采用简单粗暴的比较平均值的方法来比较两个集合:平均值大的那个集合“大于”(不管这个大于实际上代表好还是不好)平均值小的那个。
我们之所以能够这样做,其背后是正态分布。正态分布有两个性质,第一,均值和方差两个参数描述了整个分布;第二,偏离均值的部分的概率衰减的特别快(指数衰减)。同时,由于中心极限定理,保证了如果我们从原始的正态分布中一次性取出来[math]\displaystyle{ n }[/math]个样本求均值然后当做一个新的随机变量,则这个新的随机变量的方差比原来的更小[math]\displaystyle{ \sigma_n=\frac{\sigma_{1}}{\sqrt{n}} }[/math]。也就是说,这个新的随机数将更加接近原始的均值。这就保证了,如果两个正态分布函数的均值离开的足够远,两个方差足够小,例如均值之间的距离大于两个标准差之和,则两个分布函数可以看做基本上不重叠。这个意义上,大部分时候从大的分布函数中取出来的样本大于从小的分布函数中取出来的样本。
前人的工作[3][4]定义了这个每个集合(分布函数)中取出来一个样本相互比较,均值大的那个的样本大于均值小的那个的样本的几率,称为成功指数(SCI)。并且,利用成功指数来补充仅仅对比均值来更好地比较两个集合(分布函数)。
但是,这里有两个问题:第一,很多分布函数不是正态的,怎么办?用均值,甚至包含方差,来比较,就不够用了;第二,对于那些成功指数比较小的,我要是还想区分开来这两个集合,怎么办?毕竟一个均值大于另一个呢,多大意义上,这个大于是真的表示大于呢?第三,技术上,我们给SCI指数增加了一个bootstrap步骤:先从原始样本集合用有放回的bootstrap来得到L个同样的集合,对这[math]\displaystyle{ L^2 }[/math]对集合做SCI指数的计算,得到一系列的SCI指数值,对这些数值构建经验分布函数,得到95%置信区间的SCI值。同理,对于我们后面推广的多个样本比较的优劣指数,我们也需要完成这个额外的bootstrap步骤。
我们的解决方法
我们的解决方法很简单,把单样本成功指数(SCI)推广成为多样本成功指数,也就是从第一个集合(假设均值更大)中一次性取出来[math]\displaystyle{ n_{1} }[/math]个样本,从第二个集合(假设均值更小)中一次性取出来[math]\displaystyle{ n_{2} }[/math]个样本,分别算出来平均值再比较,然后,再来看,大的集合中的多样本平均值大于小的集合的多样本平均值的概率。注意到中心极限定理,这个样本数越大,得到的多样本均值的分布函数的方差越小,两个集合月容易被区分出来。因此,针对不同大小的这个成功概率([math]\displaystyle{ P\left(n_{1},n_{2}\right) }[/math])给出来了更多的两个集合相互比较的信息。我们甚至可以定义一个大小的阈值([math]\displaystyle{ \kappa_{1}, \kappa_{2} }[/math]):在这个阈值下面,[math]\displaystyle{ P\left(n_{1},n_{2}\right)\geq P_{sh} }[/math]当[math]\displaystyle{ n_{1}\gt \kappa_{1}, n_{2}\gt \kappa_{2} }[/math]。这个阈值第一起到了区分两个集合的作用,第二还能够一定程度上反映集合的元素的一致性程度,也就是元素取值越接近就会导致约值越小。
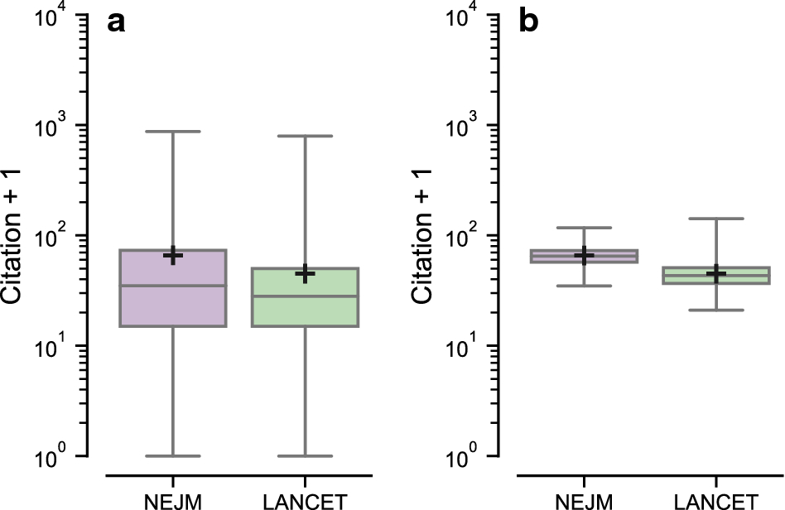
最后,我们把这个方法用到了比较期刊上去,也就是用期刊中的论文的引用次数的集合,来评价期刊。注意到这个分布是胖尾的。我们发现某些期刊的均值确实会远远大于其他期刊,但是,如果我们去计算这个“足够大才能比较”的阈值,会发现这个阈值也很大。这说明,只有当我们至少取出来这么多个样本当做整体来算均值来比较的时候,这个期刊才能够跟其他期刊来比较高低,同时这个阈值一旦真的接近期刊的大小,说明,无论如何,其实这个期刊都不应该拿来和起来期刊比较。
我们还把这个方法用到了学校的比较上去[5]。例如随机取出来一位北大的老师和师大的老师,北大老师的各方面表现(假设能算出来)高于师大的老师的可能性可能不会很高,但是,如果我们随机取出来一百位北大的老师,和另外两百位师大的老师相比较,则很可能这个成功指数会非常高。
实际上,任何一个集合的比较,都应该用我们的方法算算阈值。如果这个阈值很小,接近个位数或者远远小于集合的元素的个数,就表示,确实可以比。否则,就要考虑用我们的更加详细的比较来代替简单对比均值。
同时,我们发现,[4]的主要结论——比较两个期刊的文章的被引次数的时候,成功指数随着两个集合的均值的比值台阶性递增的函数具有普适性——的背后是文章被引次数分布函数的普适性以及其特殊形式——lognormal分布[2]。
进一步推广:一个集合的样本上某个统计结果的一致性问题
现在我们把同样的思想,bootstrap更小的集合算算,看看是否一致,找到最小的具有很大程度上一致的结果的集合大小,用到单个集合上去。
给定一个样本,算出来总样本数量(N)下计算出来的函数F(N),想看看这个结论在多大程度上是可靠的,具有比较大的一致性的。一个方法就是bootstrap,多次抽样,算出来均值和分布函数,[math]\displaystyle{ \left[\langle F\left(N\right)\rangle,\rho\left(F\left(N\right)\right)\right] }[/math]。
是不是还可以用多大足够大的思想,调整每次抽样的大小,算出来F(L),然后看看这个更小的样本上算出来的值是否和F(N)一致,或者说找到足够大的L,使得两个一致。也就是找到最小的L,使得[math]\displaystyle{ \rho\left(F\left(L\right)\right) }[/math]和[math]\displaystyle{ \rho\left(F\left(N\right)\right) }[/math]不可区分。(还是说,无论取什么样的L,两者都不可区分?如果是这样,这个方法就用不了了。试试。)
这是对bootstrap方法的简单推广。
相当于从总体数据取出来一部分数据,算算结果。如果取出来的数据比较小的时候,结论也相同(相同的概率很大),则这个结论更有说服力。
当然,理论上,还得有一个逼近定理才行。算出来的量,在整体样本越大的时候,越来越收敛。
具体应用可以是在同一个集合上,按照一种属性两个取值分成两个子集,然后比较这两个子集。一方面,可以用之前的方法,用于整个集合。另一方面,就可以用现在新的方法,先把整体集合重抽样,然后,再比较子集。
是否可区分的结果用于聚类分析
我们把两个集合在某个样本大小下的成功指数,例如一一对比、两两对比、多多对比、最大集合大小对比,都算出来。然后,取一个成功指数的阈值,凡是小于这个阈值的两个集合之间,建立连边。这样就得到了集合当做顶点,不可区分性当做连边的网络。在这个网络上做聚类,就可以得到“类内部更加不可区分”、“类之间相对更可以区分”的类。这样就把所有的集合分成了层次。
而且,我们可以采用不同大小的抽样的比较的可区分程度当成网络的权重,来做进一步的聚类。例如,用所有集合一一对比的成功指数([math]\displaystyle{ a^{i}_{j}=1-SCI^{i}_{j} }[/math])建立一个网络,聚类;用所有集合两两对比的成功指数([math]\displaystyle{ a^{i}_{j}=1-\left(CSI^{2}_{2}\right)^{i}_{j} }[/math])建立一个网络,聚类;用所有集合三三对比的成功指数([math]\displaystyle{ a^{i}_{j}=1-\left(SCI^{3}_{3}\right)^{i}_{j} }[/math])建立一个网络,聚类;等等。
是否可区分的结果用于传递排序
在排序问题(见并行排序)中,允许传递,也就是如果A优于B,B优于C,则A优于C,会增加很大的信息量。但是,这样的传递关系不一定就是正确的。能不能保证把最可靠的这样的信息传递下去,而不再传递那些不太可靠的信息呢?我们把两个集合在某个样本大小下的成功指数,例如一一对比、两两对比、多多对比、最大集合大小对比,都算出来。然后,取一个成功指数的阈值,凡是大于这个阈值的两个集合之间的排序,我们允许传递。不知道这样是否会增加可靠性,同时依靠传递最大程度上挖掘出来信息。例如通过检验在运用和不运用成功指数阈值的条件下,传递以后出现的矛盾的数量,来检验一下是否可靠性有提升。
参考文献
- ↑ Zhesi Shen, Liying Yang, Zengru Di, Jinshan Wu. Large enough sample size to rank two groups of data reliably according to their means. Scientometrics 118: 653-671 (2019). https://doi.org/10.1007/s11192-018-2995-0
- ↑ 2.0 2.1 Zhesi Shen, Liying Yang, Jinshan Wu, Lognormal distribution of citation counts is the reason for the relation between Impact Factors and Citation Success Index, Journal of Informetrics, 12(1), 153–157(2018). https://doi.org/10.1016/j.joi.2017.12.007
- ↑ Stringer, M. J., Sales-Pardo, M., & Amaral, L. A. N. (2008). Effectiveness of journal ranking schemes as a tool for locating information. PLoS ONE, 3, e1683.
- ↑ 4.0 4.1 Milojević, S., Radicchi, F., & Bar-Ilan, J. (2017). Citation success index an intuitive pair-wise journal comparison metric. Journal of Informetrics, 11, 223-231.
- ↑ Xiaoling Liu, Mihai Păunescu, Viorel Proteasa, Jinshan Wu, Minimum Representative Size in Comparing Research Performance of Universities: the Case of Medicine Faculties in Romania, Journal of Data and Information Science, 3(3),32-42(2018), https://doi.org/10.2478/jdis-2018-0013
本分类目前不含有任何页面或媒体文件。