分类:伽利略斜面实验

我们回到伽利略的时代，来面对是否“重的东西下落更快”以及“力是维持运动的原因”。关于“重的东西下落更快”，伽利略有一个看起来似乎是纯逻辑的不依赖于任何事实的思辨，或者说理想实验。他是这样设计的^[1]：让一个重物$M$和一个轻物$m$绑起来，构成一个新的重物$Mm$。按照新的重量加起来的法则，$Mm$的重量最大。于是，按照“重的东西下落更快”它具有比$M$和$m$更大的速度。现在，我们假设这两个物体是通过某种质量忽略不计的胶水或者绳子连起来构成的。我们分开来看这两个物体。$M$下落更快，$m$更慢，于是，$M$会拉动$m$使得其下落更快，$m$会拖着$M$的后腿使得其速度更慢，整体来说$Mm$的下落速度肯定介于两者之间。但是，前面我们已经得到了$Mm$下落最快的结论。自相矛盾。于是，如果逻辑论证过程没错，则原始的假设错了，因此，“重的东西下落更快”它错了。

当然，这里还有一个技术上的小问题，我们是否可以找到这样的胶水或者绳子可以把两个物体的相互影响相互传递，但是自身重量忽略不计。不过，我们总是做得到使得这个胶水或者绳子的重量远远小于$M$和$m$，于是不影响上面的论证。

那上面这个看起来似乎是纯逻辑的论证真的就反驳了“重的东西下落更快”这个结论了吗？如果可以，那么，实际上，我可以反驳任何类似的命题，例如“重的金子总价值更高”，“高个子体重更大”。你看，我说，把两块重量分别为$M$和$m$的金子绑在一起成为一块更重的金子$Mm$。如果“重的金子总价值更高”正确，则$Mm$最值钱。但是，回到分开两块来看，值钱的$M$会带动$m$使得其更值钱，不值钱的$m$会拖着$M$的后腿使得其更加不值钱。因此，值钱程度肯定在两者之间。自相矛盾。当然，我们知道后面的结论“重的金子总价值更高”在现实中往往是正确的。那问题在哪里呢？为什么我们照着同样的理由，可以被认为反驳了“重的东西下落更快”，但是，不应该被认为反驳了“重的金子总价值更高”呢？

这背后的概念其实是强度量和累积量。对于强度量，往往有前面速度那样的，快的带动慢的，慢的拖着快的后腿，如果用数学公式来表达，大概有 $v_{T}=\frac{Mv_{M}+mv_{m}}{M+m}$，而累积量却没有这个性质，反而遵循$V_{T}=V_{M}+V_{m}=Mp_{M}+mp_{m}$。其中，经常$p_{M}$是一个常数，表示例如金子的单位价格。这就能看出来，为什么速度一个强度量，肯定介于各自物体的快慢速度两者之间，但是总价一个累积量，肯定等于两者的总价相加。

也就是说，伽利略的思辨，基于了“速度是一个强度量”这个事实。问题是，这个事实又是从哪里来的呢？可能是从生活经验。因此，伽利略的看起来纯逻辑的批判实际上用了来自于现实生活经验的事实性知识。顺便，物理学永远是依赖于经验和体验的，而不是纯逻辑的。

实际上，对于重物下落更快，伽利略是如何反驳的呢？靠实验。大家都听说过的比萨斜塔的实验据考证不一定真实发生过。但是，类似于\FigRef{fig:GalileoPlane}中的斜面实验，大家相信是真的发生过的。

在\gls{name:Galileo}斜面实验中，起点处有一个单摆，然后每逢奇数的地方都有一个小钟。一个小球从起点处被释放，开始滚下来，每次撞到小钟都会发出声音。我们要把不同重量不同质地的小球拿来做这个实验，发现：对于单个小球，每次撞到钟的时间间隔相同；对于不同重量的小球，这个时间间隔也相同，不依赖于具体小球的重量。

如何来测量这个时间间隔呢？我们可以通过调整单摆的绳子长度来调整其周期，使得其振动的周期（或者周期的若干倍）正好就是小球总释放到第一个钟的时间间隔。为什么保证了这个，就可以观察到后面的时间间隔都相同，以及这个时间间隔还不依赖于小球重量呢？根据我们今天掌握的力学知识，我们知道所有小球的加速度相同，因此，每一个单位时间内速度的变化相同$v=gt$，位移（从起点开始移动的总距离）为$x=\frac{1}{2}gt^2$。按照奇数个单位长度间隔的钟的位置的设定，$x_{0}=0=0^2$，$x_{1}=0+1=1=1^2$，$x_{2}=1+3=4=2^2$，$x_{3}=4+5=9=3^2$，刚好就和$x=\frac{1}{2}gt^2$相符。也就是说，刚好背后对应着的时间间隔相同。同时，$x=\frac{1}{2}gt^2$是根据\gls{term:Newton运动定律}$F=ma$和质量和重力的关系$F=mg$得到的， \begin{align}

   a=\frac{F}{m}=\frac{mg}{m}=g.

\end{align} 因此，对于初始速度和初始位置为零的情况，$v=gt$和$x=\frac{1}{2}gt^2$，并且这个结果不依赖于物体的质量$m$。

于是，\FigRef{fig:GalileoPlane}中的斜面实验就可以展示单摆每次摆动固定的若干次，就会听到一声钟声的现象，反之亦然。

用测量的方法来研究物理对象，用比较简单的数学计算来辅助推理，从而研究和解释物理现象，这是\gls{name:Galileo}对物理学的贡献。

实际上，这个实验也可以反过来做，从实验现象发现位移和速度公式，发现加速度相同，然后，问什么样的物理模型可以得到加速度相同。我们来利用今天的手机或者相机来设计一个这样的实验。我们把手机或者相机调整为固定的拍摄间隔，例如$0.1$秒左右。也就是相机每秒钟拍摄$10$张左右的照片。买一把皮尺，长度大约一米五、两米。把皮尺固定在一个白色或者黑色的墙上。用若干个对比色明显的小球，从皮尺的起点（实际上，固定位置就可以）开始释放小球，拍摄照片。观察每张照片上小球的位置，记录下来，计算相邻两次的位置差，再计算相邻两个位置差的差。会发现，这个差基本上是一个常数。这个常数意味着什么呢？意味着加速度相同。

首先，相邻两次的位置差就代表了这一段时间间隔内的平均速度，因为每一段的时间间隔都相同的（$\bar{v}_{n}=\frac{x_{n+1}-x_{n}}{\Delta t}$）。接着，相邻两次的速度差，也就是位置差的差，就代表了这一段时间间隔内的平均加速度，$\bar{a}_{n}=\frac{v_{n+1}-v_{n}}{\Delta t}$。\FigRef{fig:FreeFall}就是实验结果和数据处理结果的照片。我们发现，确实，加速度几乎是一个常数。那按照科学研究方法，下一步，就是构建概念模型和数学模型来解释这个加速度几乎为常数的实验现象。

\begin{figure} \begin{center} \includegraphics[width=6cm]{figure/FreeFall1.jpg} \includegraphics[width=6cm]{figure/FreeFall2.jpg} \caption[自由落体实验]{自由落体实验。我们用相机、皮尺和小球完成了自由落体实验，记录数据，并且得到平均加速度的值。\remark{拍摄实验现象图和数据处理图。}} \FigLabel{fig:FreeFall} \end{center} \end{figure}

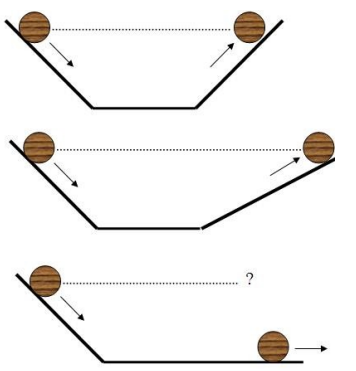
有了斜面这个实验装置，对“力是维持运动的原因”的突破就是相对简单的事情了。我们今天知道，只要做一个从斜面上滑下来的小球在不同粗糙程度的平面上运动的实验，就可以发现，平面越光滑则小球在到达平面以后运动的距离越远。第一，这个运动，不受额外的推力的作用，但是会维持很长时间，因此就否定了“力是维持运动的原因”。不过，这个实验牵涉到\gls{name:Aristotle}和\gls{name:Galileo}的含混不清力的概念的问题，应该是没有被\gls{name:Galileo}真的做过的。至少在《关于两门新科学的对话》\cite{Galileo:Dialogue2}中没有这个明确的记录。第二，我们可以进一步猜测，如果平面可以无限光滑，没有摩擦力，那么，可能这个运动会一直持续下去。实际上，这个第二点，\gls{name:Galileo}可能是做了实验的，或者至少是做了理想实验的\cite{Galileo:Dialogue2}。\gls{name:Galileo}让一个斜面接上一个不同角度的斜面，\FigRef{fig:GalileoSlope}，说如果没有摩擦力，可以推断，其在小球在更平的斜面上的运动的距离更远——对于角度更小的直角三角形要达到相同的高度需要更长的斜边。因此，如果这个角度完全为零，则肯定需要运动到无穷远处。当然，如果回到有摩擦力的情形，我们原则上就可以来完成前面的不同光滑程度也就是具有不同摩擦力的实验来否定“力是维持运动的原因”以及推断无限光滑会使得小球一直运动下去。

\begin{figure} \begin{center} \includegraphics[width=8cm]{figure/GalileoSlope.png} \caption[Galileo斜面实验看运动距离]{\gls{name:Galileo}斜面实验看运动距离。\gls{name:Galileo}把不同角度的斜面接起来，假设没有摩擦，来推断在完全水平的表面上运动的距离。\remark{图重新做。}} \FigLabel{fig:GalileoSlope} \end{center} \end{figure}

我们看到，\gls{name:Aristotle}和\gls{name:Galileo}都注意从生活经验中提炼问题和答案，但是在\gls{name:Galileo}这里，最大的变化就是要对生活经验做测量，开展实验研究，以及基于实验数据来开展计算和思考。

不过，真正发挥实验数据的价值，还得靠进一步的数学计算和分析，以及数学建模。这就得看\gls{name:Kepler}和\gls{name:Newton}的了。

参考文献