定义和含义

“重物下落更快”是一个迷思，其含义是“在离地面相同的距离释放一个更重的物体和一个更轻的物体，则更重的物体先到达地面”，还可以指下面这个推广了的含义“在离地面相同的距离释放一个更重的物体和一个更轻的物体，在下落过程中的每一个位置点上，重物的速度大于轻物的速度”。这个迷思来源于对日常生活经验的不完全的总结。

实际上，如果不考虑空气阻力等其他因素，仅仅考虑地球对物体的引力，也就是重力的话，物体下落的速度和时间和物体的重量（物理学区分质量——物质的量——和重量）没有关系。不过，这个知识本身是对逻辑上和学科知识上都要求更高的知识。学习者完全可以从另一个角度，也就是对生活经验的更加完善的总结，以及对“一个规律应该尽可能多地描述事物”的追求，来解除这个迷思。

概念地图

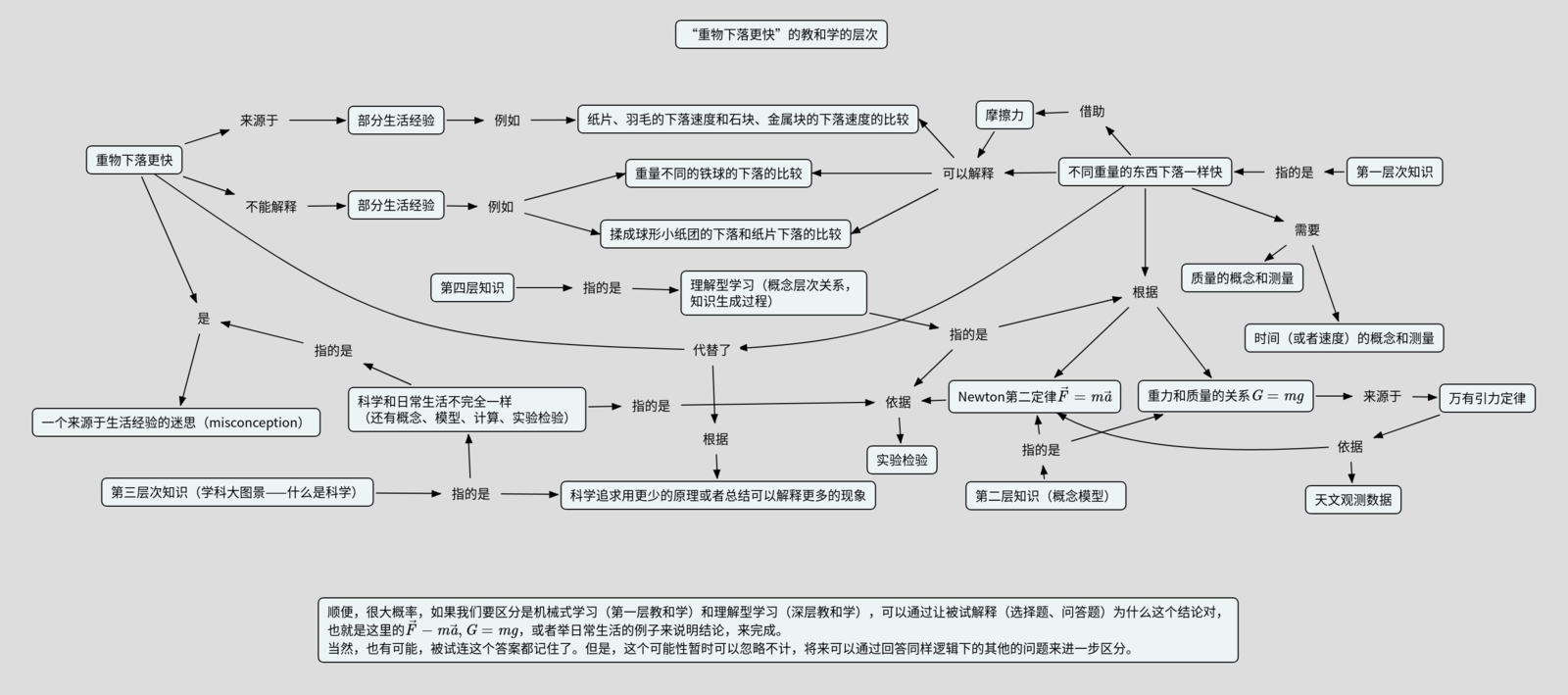
乘法的概念地图（图的格式将来改成嵌入文本的格式，用户既可以直接下载图，还可以获取这个概念地图的文本文件）：

教和学的层次

在定理和逆否定理的关系的教学中，如果主要任务就是让学生记住和会在简单的接近生活的实际场景中运用“定理和逆否定理等价”，则属于第一层教和学——事实性和流程性知识的教和学。例如，在上面的概念地图中，我们用具体的“喝酒的人的年龄必须大于等于18岁”为例，展示了其等价的描述“年龄小于18岁的不能喝酒”。并且，在这个例子上，我们编了一个问题来解决一下，“如果你可以选择”

一旦，我们从这个具体例子，走到更加一般的条件[math]\displaystyle{ P,Q }[/math]的语言，也就是喝酒年龄问题背后的数学概念，则基于这样的从具体到抽象，从抽象到具体的过程的教和学，就是第二层次的教和学。更进一步，可以问这个抽象语言[math]\displaystyle{ P,Q }[/math]表达的定理和逆否定理等价怎么就能够回答要检测什么的问题。这也是第二层次的教和学，不过是用同层次内更加高层的知识来理解同层次内相对浅层的知识。乃至于，再进一步，我们可以追问为什么原定理和逆否定理会等价，然后用集合论的语言来证明和理解这个等价性，这也是第二层次的教和学，不过就是用同一层次内更加高层的知识来理解同层次内相对浅层的知识。

不过，跳出这个具体知识，我们看到，从集合论的语言到原命题和逆否命题的等价性，从原命题和逆否命题的等价性来做出来如何检测的选择，分别反映了“数学知识的系统性”、“逻辑推理是数学论证的重要形式，数学需要讲究论证”，这些关于数学的学科大图景的内容。这就属于第三个层次的知识。

再进一步，数学论证反映了批判性思维，从知识生成的过程来理解知识反映了理解型学习，这些超越具体学科的一般思维方式和学习方法，这属于第四个层次的知识。

中小学阶段的理解

至少要达到具象层面的第二层的理解，也就是用具体例子的语言来体会到“原定理和逆否定理”的等价性。如果进一步到抽象层面的第二层就更好了，也就是可以用抽象语言的“原定理和逆否定理”来看到一类具体问题背后的相同的逻辑。

尽量达到第三层的理解，也就是从这些例子体会到数学论证、数学知识的系统性。

如果还能够走到第四层，也就是数学概念的学习需要依靠系联性思考、批判性思维、以知识生成器为目标的理解型学习，那就更好了。